Citizen SR-281N: Zawarto ść
Zawarto ść: Citizen SR-281N

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po1-
Kalkulator Naukowy / Instrukcja Obs
ł
ugi ........................................ 2
W
łą
czanie i wy
łą
czanie..................................................................... 2
Wymiana baterii................................................................................ 2
Funkcja automatycznego wy
łą
czania ............................................... 2
Operacja Reset ................................................................................ 2
Dostosowanie kontrastu ................................................................... 3
Odczyt wy
ś
wietlacza ........................................................................ 3
Zanim rozpoczniesz obliczenia ........................................................ 4
Korzystanie z klawiszy " MODE " ..................................................... 4
Korzystanie z klawiszy " 2nd " .......................................................... 4
Dokonywanie korekt ......................................................................... 4
Cofni
ę
cie operacji............................................................................. 4
Funkcja powtarzania operacji ........................................................... 5
Obliczenia wykorzystuj
ą
ce pami
ęć
................................................... 5
Kolejno
ść
operacji ............................................................................ 6
Dok
ł
adno
ść
i pojemno
ść
................................................................... 7
B
łę
dy ................................................................................................ 9
Obliczenia podstawowe .................................................................... 9
Obliczenia arytmetyczne .................................................................. 9
Obliczenia z wykorzystaniem nawiasów......................................... 10
Obliczenia procentów ..................................................................... 11
Wy
ś
wietlanie liczb .......................................................................... 11
Obliczenia funkcji naukowych ....................................................... 13
Logarytmy i antylogarytmy.............................................................. 13
Dzia
ł
ania na u
ł
amkach ................................................................... 13
Konwersja jednostek miar k
ą
tów .................................................... 14
Konwersja zapisu sze
ść
dziesi
ę
tnego do dziesi
ę
tnego i na odwrót. 15
Funkcje trygonometryczne i odwrotne trygonometryczne.............. 15
Funkcje hiperboliczne i odwrotne hiperboliczne. ............................ 16
Transformacje wspó
ł
rz
ę
dnych ........................................................ 16
Prawdopodobi
ęń
stwo ..................................................................... 17
Inne funkcje ( 1/x,
,
3
,
X
, x
2
, x
3
, x
y
, INT, FRAC ) ............... 18
Konwersja jednostek ...................................................................... 19
Sta
ł
e fizyczne ................................................................................. 19
Obliczenia w trybie Base–n ............................................................ 25
Konwersja liczb .............................................................................. 26
Funkcja bloków............................................................................... 26
Operacje arytmetyczne w róznych uk
ł
adach .................................. 27
Warto
ś
ci ujemne............................................................................. 27
Operacje logiczne........................................................................... 27
Obliczenia statystyczne .................................................................. 28
Wprowadzenie danych ................................................................... 28
Wy
ś
wietlanie wyników .................................................................... 29
Kasowanie danych ......................................................................... 32
Korygowanie danych ...................................................................... 32
Komunikat FULL............................................................................. 33
Operacje na liczbach zespolonych ................................................ 33
Zawarto ść

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po2-
Kalkulator Naukowy / Instrukcja Obs
ł
ugi
W
łą
czanie i wy
łą
czanie
Aby w
łą
czy
ć
kalkulator, naci
ś
nij [ ON/C ] ;
Aby wy
łą
czy
ć
kalkulator,
naci
ś
nij [ 2nd ] [ OFF ].
Wymiana baterii
Kalkulator zasilany jest dwiema bateriami alkalicznymi typu G13
(LR44). Je
ś
li tekst na wy
ś
wietlaczu jest s
ł
abo widoczny, to nale
ż
y
bezzw
ł
ocznie wymieni
ć
baterie. Uwa
ż
aj, by podczas wymiany baterii
nie zrobi
ć
sobie krzywdy.
1. Wykr
ę
ci
ć
ś
rubki z ty
ł
u kalkulatora.
2. Wstawi
ć
p
ł
aski
ś
rubokr
ę
t w szpar
ę
pomi
ę
dzy doln
ą
a górn
ą
cz
ęś
ci
ą
pokrywy i delikatnie przekr
ę
ci
ć
go, aby zdj
ąć
pokryw
ę
.
3. Wyj
ąć
i wyrzuci
ć
obie baterii. Nigdy nie nale
ż
y pozwala
ć
dzieciom
bawi
ć
si
ę
bateriami.
4. Przetrze
ć
nowe baterie such
ą
szmat
ą
aby zapewni
ć
dobry kontakt.
5. W
ł
o
ż
y
ć
nowe baterie p
ł
ask
ą
stron
ą
(plus) do góry.
6. Wyrówna
ć
górn
ą
i don
ą
cze
ś
ci pokrywy i zamkn
ąć
j
ą
.
7. Zakr
ę
ci
ć
ś
rubki.
Funkcja automatycznego wy
łą
czania
Kalkulator wy
łą
cza si
ę
automatycznie je
ś
li nie jest u
ż
ywany w ci
ą
gu
oko
ł
o 6~9 minut.
Kalkulator mo
ż
e by
ć
reaktywowany naci
ś
ni
ę
ciem
klawisza [ ON/C ]; wszyskie wskazania wy
ś
wietlacza i ustawienia
pami
ę
ci zachowuj
ą
si
ę
.
Operacja Reset
Je
ś
li kalkulator jest w
łą
czony, ale wy
ś
wietla b
łę
dny wynik, naci
ś
nij
kolejno klawisze [ MODE ] [ 4 ] ( RESET ).
Na wy
ś
wietlaczu pojawi
si
ę
komunikat z pro
ś
b
ą
potwierdzenia zresetowania kalkulatora i
wyczyszczenia zawarto
ś
ci pami
ę
ci.
RESET :
N Y
Przesu
ń
kursor na ‘Y ‘ naci
ś
ni
ę
ciem [ ], a potem naci
ś
nij klawisz
[ = ] aby wyczy
ś
ci
ć
wszystkie zmienne, programy, operacje
oczekuj
ą
ce na wykonanie, dane statystyczne, odpowiedzi, wszystkie
wprowadzone dane, ca
łą
zawarto
ść
pami
ę
ci;
aby zrezygnowa
ć
z
operacji resetowania wybierz " N ".
Je
ś
li kalkulator zawiesi
ł
si
ę
i wykonanie oblicze
ń
jest niemo
ż
liwe,
nale
ż
y nacisn
ąć
przycisk RESET w zag
łę
bieniu przy pomocy
cienkiego przedmiotu, aby zlikwidowa
ć
b
łą
d. Spowoduje to powrót do
ustawie
ń
fabrycznych kalkulatora.

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po3-
Dostosowanie kontrastu
Naci
ś
ni
ę
cie klawiszy [ – ] lub [ + ], a nast
ę
pnie klawisza [ MODE ]
pozwala zmieni
ć
kontrast wy
ś
wietlacza na ja
ś
niejszy lub ciemniejszy.
D
ł
u
ż
sze przytrzymywanie wci
ś
ni
ę
tego klawisza spowoduje,
ż
e
wy
ś
wietlacz odpowiednio rozja
ś
ni si
ę
lub przyciemni si
ę
.
Odczyt wy
ś
wietlacza
Wy
ś
wietlacz ma dwie lini
ę
danych i wska
ź
ników
Linia wprowadzania
danych pozwala na wprowadzenie 128 cyfr.
W dolnej linii ukazuj
ą
si
ę
wyniki oblicze
ń
o d
ł
ugo
ś
ci do 12 cyfr oraz 2-cyfrowy dodatni lub
ujemny wyk
ł
adnik.
Po wprowadzeniu równania i naci
ś
ni
ę
ciu klawisza [ = ] równanie
uka
ż
e si
ę
w gornej linii, a wynik oblicze
ń
w dolnej.
Aktualny tryb pracy kalkulatora sygnalizowany jest w linii wska
ź
ników
wy
ś
wietlacza nast
ę
puj
ą
cymi wska
ź
nikami:
Wska
ź
nik
Znaczenie
M Niezale
ż
na pami
ęć
–
Wynik jest ujemny
E B
łą
d
STO
Aktywny tryb zapisu zmiennych
RCL
Aktywny tryb przywo
ł
ywania zmiennych z pami
ę
ci
2nd
Aktywny drugi zestaw klawiszy funkcjonalnych
HYP
Tryb hiperbolicznych funkcji trygonometrycznych
ENG Wy
ś
wietlanie wyników w trybie in
ż
ynierskim
CPLX
Aktywny tryb liczb zespolonych
CONST Sta
ł
e fizyczne
DEGRAD
Tryb wyboru jednostek k
ą
tów:
DEG –stopnie
(DEGrees), GRAD – grady (GRADs), RAD – radiany
(RADs)
BIN Liczby
dwójkowe
OCT Liczby
ósemkowe
HEX Liczby
szestnastkowe
( )
Otwieranie nawiasów
TAB Wy
ś
wietlanie wyników z ustalon
ą
liczb
ą
cyfr po
przecinku
STAT
Aktywny tryb oblicze
ń
statystycznych
REG
Tryb obliczenia regresji
EDIT
Tryb edycji danych
CPK
CPK : Istotno
ść
procesu
CP
:
Poziom istotno
ś
ci
USL
Górna granica poziomu istotno
ś
ci
LSL
Dolna granica poziomu istotno
ś
ci
i Cz
ęść
urojona
Cofni
ę
cie operacji (undo)

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po4-
Zanim rozpoczniesz obliczenia
Korzystanie z klawiszy " MODE "
Naciskaj
ą
c klawisz [ MODE ], mo
ż
na wy
ś
wietli
ć
menu zmiany trybu.
Do wyboru mamy kilka podstawowych trybów operacyjnych: ( " 1
MAIN ", " 2 STAT ", " 3 CPLX ", " 4 RESET " ) oraz notacj
ę
in
ż
yniersk
ą
( " 5 ENG " ).
1 MAIN :
S
ł
u
ż
y do wykonywania oblicze
ń
podstawowych, w tym
naukowych i Base-n.
2 STAT :
S
ł
u
ż
y do oblicze
ń
statystycznych z jedn
ą
i dwiema
zmiennymi, oraz obliczenia regrecji.
3 CPLX :
S
ł
u
ż
y do oblicze
ń
na liczbach zespolonych.
4 RESET : S
ł
u
ż
y do resetowania kalkulatora.
5 ENG :
S
ł
u
ż
y do oblicze
ń
in
ż
ynierskich, w notacji in
ż
unierskiej.
Pozpatrzmy jako pryk
ł
ad korzystanie z trybu " 2 STAT " :
Sposób 1 :
Naci
ś
nij klawisz [ MODE ] a potem przesu
ń
kursor na
żą
dan
ą
pozycj
ę
naciskaj
ą
c odpowiednio klawisze [
]
lub [ 2nd ] [
] doputy, dopóki nie zostanie
podkre
ś
lona pozycja " 2 STAT ", a potem naci
ś
nij klawisz
[ = ].
Sposób 2 :
Naci
ś
nij klawisz [ MODE ], a potem wprowad
ź
bezpo
ś
rednio numer trybu pracy [ 2 ].
Korzystanie z klawiszy " 2nd "
Po nacisni
ę
ciu klawisza [ 2nd ] w linii wska
ź
ników pojawi si
ę
napis
"2nd".; oznacza to,
ż
e kalkulator oczekuje na wprowadzenie funkcji.
Je
ś
li nacisn
ą
le
ś
[ 2nd ] przypadkowo, to powtórne wci
ś
ni
ę
cie klawisza
[ 2nd ] przywróci u
ż
ywany poprzednio tryb.
Dokonywanie korekt
Je
ś
li pope
ł
nile
ś
b
łą
d wprowadzaj
ą
c liczb
ę
(ale nie naci
ś
n
ą
le
ś
klawisza
dzialania arytmetycznego), naci
ś
nij klawisz [ CE ] aby skasowa
ć
niepotrzebn
ą
cyfr
ę
lub wykasuj pojedy
ń
cze cyfry za pomoc
ą
klawisza
[
], lub wyczy
ść
wsystkie dane za pomoc
ą
[ ON/C ].
Po wprowadzeniu wszystkich korekt naci
ś
nij klawisz [ = ] aby
otrzyma
ć
wynik.
Naci
ś
ni
ę
ciem klawisza [ ON/C ] mo
ż
na wykasowa
ć
ostatni wynik oblicze
ń
(za wyj
ą
tkiem tego, co zapisano w pami
ę
ci).
Je
ś
li zrobile
ś
b
łą
d, naciskaj
ą
c niew
ł
asciwy klawisz dzialania
arytmetycznego, po prostu naci
ś
nij w
ł
a
ś
ciwy.
Cofni
ę
cie operacji
Ta funkcja pozwala korygowa
ć
niektóre b
łę
dy.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po5-
Je
ś
li cyfr
ę
wykasowano za pomoc
ą
klawiszy [ ], [ CE ] lub [ ON/C ],
na ekranie wy
ś
wietla si
ę
wska
ź
nik "
"; oznacza to,
ż
e mo
ż
esz
cofn
ąć
operacje, naciskaj
ą
c [ 2nd ] [
].
Funkcja powtarzania operacji
Funkcja ta pozwala prze
ś
ledzi
ć
ostatnio wykonywane operacje.
Naci
ś
ni
ę
cie klawiszy [ ] lub [ 2nd ] [
] po wykonaniu oblicze
ń
powoduje wy
ś
wietlenie ostatnio wykonanej operacji.
Nacisni
ę
cie [ ]
powoduje wy
ś
wietlenie wszystkich operacji od pocz
ą
tku do ko
ń
ca, a
kursor znajduje si
ę
nad pierwsz
ą
cyfr
ą
.
Nacisni
ę
cie [ 2nd ] [
]
powoduje wy
ś
wietlenie wszystkich operacji od ko
ń
ca, a kursor
znajdzie sie w pozycji po ostatnie cyfrze.
Przesuwaj
ą
c kursor za
pomoc
ą
klawiszy [ ] lub [ 2nd ] [
] mo
ż
na edytowa
ć
dane lub
polecenia.
Obliczenia wykorzystuj
ą
ce pami
ęć
Pami
ęć
zmiennych
W kalkulatorze jest 9 standardowych rejestrów dla zapami
ę
tywania
zmiennych: A, B, C, D, E, F, M, X, Y.
W dowolnym z tych rejestrów
mo
ż
na przechowywa
ć
liczb
ę
rzeczywist
ą
.
•
Polecenie [ STO ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] pozwala zapisa
ć
zmienne do pami
ę
ci.
•
Polecenie [ RCL ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] wy
ś
wietla
warto
ść
zmiennej, pobran
ą
z pami
ę
ci.
•
Polecenie [ 0 ] [ STO ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] zeruje
odpowiedni rejestr pami
ę
ci.
¾
(1) Wprowad
ź
warto
ść
30 do rejestru A
DEG
3 0
Æ
A
30 [ STO ] [ A ]
3 0
.
¾
(2) Pomno
ż
y
ć
zmienn
ą
A przez 5 i zapisa
ć
wynik do rejestru B
DEG
5
¼
A =
5 [ x ] [ RCL ] [ A ] [ = ]
1 5 0
.
DEG
1 5 0
Æ
B
[ STO ] [ B ]
1 5 0 .
¾
(3) Wyczy
ś
ci
ć
zawarto
ść
rejestru B
DEG
0
Æ
B
0 [ STO ] [ B ]
0
.
DEG
B =
[ RCL ] [ B ] [ = ]
0
.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po6-
Niezale
ż
na pami
ęć
U
ż
ywaj
ą
c niezale
ż
n
ą
pami
ęć
powiniene
ś
przestrzega
ć
nast
ę
puj
ą
cych
zasad:
• Naci
ś
nij klawisz [ M+ ] aby doda
ć
wynik do pami
ę
ci. Na ekranie
pojawi si
ę
wska
ź
nik " M ".
Aby wy
ś
wietli
ć
liczb
ę
przechowywan
ą
w
pami
ę
ci, naci
ś
nij klawisz [ MR ].
• Przywo
ł
ywanie przechowywanej w pami
ę
ci liczby naci
ś
ni
ę
ciem
klawisza [ MR ] nie wp
ł
ywa na zawarto
ść
rejestru pami
ę
ci.
• Niezale
ż
na pami
ęć
jest niedost
ę
pna w trybie oblicze
ń
statystystycznych.
• Pami
ęć
zmiennych M i niezale
ż
na pami
ęć
wspó
ł
u
ż
ytkuj
ą
te same
rejestry.
• Aby zast
ą
pi
ć
liczb
ę
zapisan
ą
w pami
ę
ci liczb
ą
wy
ś
wietlon
ą
na
ekranie, nale
ż
y nacisn
ąć
klawisz [ X M ].
• Aby wykasowa
ć
niezale
ż
n
ą
pami
ęć
, nale
ż
y nacisn
ąć
kolejno
klawisze [ 0 ] [ X M ], [ ON/C ] [ X M ] lub [ 0 ] [ STO ] [ M ].
¾
[ ( 3 x 5 ) + ( 56 7 ) + ( 74 – 8 x 7 ) ] = 41
DEG
0 [ X M ]
0
.
DEG
7 4 – 8
¼
7 M +
3 [ x ] 5 [ M+ ] 56 [ ] 7 [ M+ ] 74
[ – ] 8 [ x ] 7 [ M+ ]
M
1 8
.
DEG
M
[ MR ]
M
4 1
.
DEG
0 [ X M ]
0
.
(Uwaga) :
Oprócz klawiszy [ STO ] lub [ X M ] do zapisywania
warto
ś
ci zmiennej M mo
ż
na pos
ł
u
ż
y
ć
si
ę
tak
ż
e klawiszem
[ M+ ].
Podczas nacisni
ę
cia klawiszy [ STO ] [ M ] lub
[ X M ] warto
ść
zapisana wcze
ś
niej w pami
ę
ci zmiennych
M zostanie wykasowana i zast
ą
piona now
ą
warto
ś
ci
ą
.
Naci
ś
ni
ę
cie klawisza [ M+ ] doda
ć
liczb
ę
do zapisanej w
pami
ę
ci.
Kolejno
ść
operacji
Obliczenia dokonywane s
ą
w nast
ę
puj
ą
cej kolejno
ś
ci :
1) U
ł
amki
2) Wyra
ż
enia zawarte w nawiasach.
3) Transformacja
wspó
ł
rz
ę
dnych ( P R , R P )
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po7-
4) Funkcje typu A, które wymagaj
ą
wprowadzenia warto
ś
ci
argumentu przed wci
ś
ni
ę
ciem klawisza funkcyjnego, na przyk
ł
ad,
x
2
, 1/x,
π
, x!, %, RND, ENG,
,
, x ', y '.
5) x
y
,
X
6) Funkcje Typu B, których wprowadzenie wymaga naci
ś
ni
ę
cia
klawiszy funkcyjnych, na przyk
ł
ad, sin, cos, tan, sin
–1
, cos
–1
,
tan
–1
, sinh, cosh, tanh, sinh
–1
, cosh
–1
, tanh
–1
, log, ln, FRAC,
INT,
√
,
3
, 10
X
, e
X
, NOT, EXP, DATA w trybie STAT.
7) +/–,
NEG
8) nPr, nCr
9) x
,
10) +, –
11) AND, NAND –-- tylko w trybie Base–n
12) OR, XOR, XNOR --- tylko w trybie Base–n
Dok
ł
adno
ść
i pojemno
ść
D
ł
ugo
ść
wy
ś
wietlanych liczb :
Do 12 cyfr
D
ł
ugo
ść
liczb podczas operacji :
Do 14 cyfr
W ogólno
ś
ci wynik ka
ż
dego obliczenia wy
ś
wietlany jest w postaci 12-
cyfrowej mantysy lub 12-cyfrowej mantysy oraz 2-cyfrowego
wyk
ł
adnika pot
ę
gi tzn do 10
± 99
.
Liczby wprowadzane jako argumenty funkcji musz
ą
by
ć
zawarte w
przedziale okre
ś
lono
ś
ci funkcji:
Funkcje Przedzia
ł
sin x
cos x
tan x
Deg :
x
<
4.5 x 10
10
deg
Rad :
x
<
2.5 x 10
8
π
rad
Grad :
x
<
5 x 10
10
grad
jednak
ż
e, dla tan x
Deg :
x
≠
90 (2n+1)
Rad :
x
≠
2
π
(2n+1)
Grad :
x
≠
100 (2n+1), (n liczba
ca
ł
kowita)
sin
–1
x, cos
–1
x
x
≦
1
tan
–1
x
x
<
1 x 10
100
sinh x, cosh x
x
≦
230.2585092
tanh x
x
<
1 x 10
100
sinh
–1
x
x
<
5 x 10
99
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po8-
cosh
–1
x
1
≦
x
<
5 x 10
99
tanh
–1
x
x
<
1
log x, ln x
1 x 10
–99
≦
x
<
1 x 10
100
10
x
–1 x 10
100
<
x
<
100
e
x
–1 x 10
100
<
x
≦
230.2585092
x
0
≦
x
<
1 x 10
100
x
2
x
<
1 x 10
50
x
3
x
<
2.15443469003 x 10
33
1/x
x
<
1 x 10
100
, x
≠
0
3
x
x
<
1 x 10
100
x !
0
≦
x
≦
69, x liczba ca
ł
kowita.
R P
2
2
y
+
x
<
1 x 10
100
P R
0
≦
r
<
1 x 10
100
Deg
:
│
θ
│
<
4.5 x 10
10
deg
Rad
:
│
θ
│
<
2.5 x 10
8
π
rad
Grad
:
│
θ
│
<
5 x 10
10
grad
jednak
ż
e, dla tan x
Deg
:
│
θ
│
≠
90 (2n+1)
Rad
:
│
θ
│
≠
2
π
(2n+1)
Grad :
│
θ
│
≠
100 (2n+1), (n liczba ca
ł
kowita)
│
D
│
, M, S
<
1 x 10
100
, 0
≦
M, S
x
<
1 x 10
100
x
y
x
>
0 : –1 x 10
100
<
y log x
<
100
x = 0 : y
>
0
x
<
0 : y = n, 1/(2n+1), n liczba ca
ł
kowita.
lecz –1 x 10
100
<
y log
│
x
│
<
100
x
y
y
>
0 : x
≠
0, –1 x 10
100
<
x
1
log y
<
100
y = 0 : x
>
0
y
<
0 : x=2n+1, l/n, n liczba ca
ł
kowita. (n
≠
0)
lecz –1 x 10
100
<
x
1
log
│
y
│
<
100
a b/c
Wprowadzanie: cz
ęść
ca
ł
kowita liczby,
licznik i mianownik nie mog
ą
przekroczy
ć
12 cyfr (w
łą
cznie z przecinkiem dziesi
ę
tnym)
Wynik : Je
ś
li cz
ęść
ca
ł
kowita liczby, licznik i
mianownik nie przekraczaj
ą
1 x 10
12
, to
wynik b
ę
dzie wy
ś
wietlony w postaci u
ł
amka
nPr, nCr
0
≦
r
≦
n, n
≦
10
100
, n,r – liczby ca
ł
kowite.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po9-
STAT
x
<
1 x 10
50
,
y
<
1 x 10
50
σ
x,
σ
y,
x
, y ,a, b, r : n
≠
0 ;
Sx, Sy
:
n
≠
0, 1 ; x
n
= 50 ; y
n
= 50 ;
Liczba powtórze
ń
≤
255, n liczba ca
ł
kowita.
DEC
– 2147483648
≦
x
≦
2147483647
BIN
0
≦
x
≦
01111111111111111111111111111111 (dla
zera i liczb dodatnich)
10000000000000000000000000000000
≦
x
≦
11111111111111111111111111111111
(dla liczb ujemnych)
OCT
0
≦
x
≦
17777777777 (dla zera lub liczb
dodatnich)
20000000000
≦
x
≦
37777777777
(dla liczb ujemnych)
HEX
0
≦
x
≦
7FFFFFFF ( dla zera lub liczb
dodatnich)
80000000
≦
x
≦
FFFFFFFF (dla liczb
ujemnych)
B
łę
dy
Komunikat o wyst
ą
pieniu b
łę
du (symbol "
E
" ) pojawia si
ę
na
wy
ś
wietlaczu, a dalsze operacje s
ą
zawieszane w przypadkach gdy
zaistniej
ą
wymienione poni
ż
ej warunki.
1) Próba dzielenia przez 0.
2) Wprowadzony argument wychodzi po za granicy okre
ś
lono
ś
ci
funkcji.
3) Kiedy wynik oblicze
ń
przewy
ż
sza dopuszczalny zakres.
4) Liczba nawiasów [ ( ] w wyra
ż
eniu przewy
ż
sza 13 na jednym
poziomie.
5) Je
ś
li warto
ść
USL
<
LSL
Aby zlikwidowa
ć
wy
ż
ej wymienione b
łę
dy, nale
ż
y nacin
ąć
klawisz
[ ON/C ].
Obliczenia
podstawowe
Do oblicze
ń
podstawowych s
ł
u
ż
y tryb MAIN ( [ MODE ] 1
( MAIN ) ).
Obliczenia arytmetyczne
Operacje arytmetyczne wykonywane s
ą
w tej kolejno
ś
ci, w jakiej
zapisane s
ą
w wyra
ż
eniu.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po10-
¾
7 + 5 x 4 = 27
DEG
7 + 5
¼
4 =
7 [ + ] 5 [ x ] 4 [ = ]
2 7
.
Dla warto
ś
ci ujemnych naci
ś
nij [ +/– ] po wprowadzeniu liczby;
Mantys
ę
i wyk
ł
adnik mo
ż
na wprowadzi
ć
w postaci wyk
ł
adniczej za
pomoc
ą
klawisza [ EXP ].
¾
2.75 x 10
– 5
= 0.0000275
DEG
2
.
7 5 E – 0 5 =
2.75 [ EXP ] 5 [ +/– ] [ = ]
0
.
0 0 0 0 2
7 5
Wyniki przewy
ż
szaj
ą
ce 10
12
lub mniejsze od 10
–11
wy
ś
wietlane s
ą
w
postaci wyk
ł
adniczej.
¾
12369 x 7532 x 74010 = 6895016425080
= 6.89501642508 x 10
12
DEG
1 2 3 6 9
¼
7 5 3 2
¼
7
12369 [ x ] 7532 [ x ] 74010
[=]
6
.
8 9 5 0 1 6 4 2 5 0 8
12
Obliczenia z wykorzystaniem nawiasów
Wyra
ż
enia zawarte w nawiasach zawsze wykonywane s
ą
w pierwszej
kolejno
ś
ci.
W kalkulatorach
SR-281N
mo
ż
na u
ż
ywa
ć
w jednym
obliczeniu do 13 poziomów nawiasów wewn
ę
trznych.
Mo
ż
na zrezygnowa
ć
z zamkni
ę
cia nawiasu (nawiasów)
wyst
ę
puj
ą
cych na ko
ń
cu wyra
ż
enia; w tym przypadku liczba
pomini
ę
tych nawiasów nie ma znaczenia.
¾
2 x { 7 + 6 x ( 5 + 4 ) } = 122
DEG
2
¼
( 7 + 6
¼
( 5 + 4 =
2 [ ( ] 7 [ + ] 6 [ ( ] 5 [ + ] 4 [ = ]
1 2 2
.
(Uwaga) : Znak "
x
" bezpo
ś
rednio przed nawiasem mo
ż
na omin
ąć
.
Nie mo
ż
na uzyska
ć
prawid
ł
owego wyniku naciskaj
ą
c [ ( ] 2 [ + ] 3 [ ) ]
[ EXP ] 2.
W tym przyk
ł
adzie nale
ż
y wprowadzi
ć
[ x ] pomi
ę
dzy [ ) ] a
[ EXP ].
¾
( 2 + 3 ) x 10
2
= 500
DEG
( 2 + 3 )
¼
1 E 0 2 =
[ ( ] 2 [ + ] 3 [ ) ] [ x ] [ EXP ] 2
[ = ]
5
0 0
.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po11-
Obliczenia procentów
Wynikiem naciskania klawiszy [ 2nd ] [ % ] b
ę
dzie dzielenie
wprowadzonej liczby przez 100.
Ta kolejno
ść
naciskania klawiszy
mo
ż
e by
ć
u
ż
ywana dla oblicze
ń
odsetek, dodatków, rabatów i
stosunków procentowych.
¾
120 x 30 % = 36
DEG
1 2 0
¼
3 0 % =
120 [ x ] 30 [ 2nd ] [ % ] [ = ]
3 6
.
¾
88 55 % = 160
DEG
8 8
5 5 % =
88 [ ] 55 [ 2nd ] [ % ] [ = ]
1 6 0
.
Wy
ś
wietlanie liczb
W kalkulatorze mo
ż
na u
ż
ywa
ć
kilka formatów wy
ś
wietlania liczb.
Stala liczba cyfr po przecinku / Format zmiennoprzecinkowy
Aby wybra
ć
liczb
ę
miejsc po przecinku dzisi
ę
tnym, naci
ś
nij klawisze
[ 2nd ] [ TAB ] i cyfr
ę
od 0 do 9.
Wy
ś
wietlane na ekranie liczby b
ę
d
ą
zaokr
ą
glone do ustalonej liczby miejsc po przecinku.
Aby wróci
ć
w
tryb zmiennoprzecinkowy, nale
ż
y nacisn
ąć
[ 2nd ] [ TAB ] [ • ].
Tryb naukowy
Aby zmieni
ć
wy
ś
wietlanie liczb z trybu zmiennoprzecinkowego na
naukowy i na odwrót, nale
ż
y nacisn
ąć
klawisz [ F
↔
E ].
Format in
ż
ynierski
Naci
ś
ni
ę
ciem klawisza [ ENG ] lub kolejno klawiszy [ 2nd ] [ ]
mo
ż
emy wy
ś
wietla
ć
wyk
ł
adnik jako wielokrotno
ść
liczby 3.
¾
6 7 = 0.85714285714…
DEG
6
7 =
6 [ ] 7 [ = ]
0
.
8 5 7 1 4 2 8 5 7 1 4
DEG TAB
6
7 =
[ 2nd ] [ TAB ] 4
0 . 8 5 7 1
DEG TAB
6
7 =
[ 2nd ] [ TAB ] 2
0
.
8 6
DEG
6
7 =
[ 2nd ] [ TAB ] [ • ]
0
.
8 5 7 1 4 2 8 5 7 1 4
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po12-
DEG
6
7 =
[ F
↔
E ]
8
.
5 7 1 4 2 8 5 7 1 4 3
–01
DEG
[ ENG ]
8 5 7
.
1 4 2 8 5 7 1 4 3
–03
DEG
[ 2nd ] [
] [ 2nd ] [
]
0
.
0 0 0 8 5 7 1 4 2 8 5
03
Symbole trybu in
ż
ynierskiego (ENG)
W trybie in
ż
ynierskim (ENG) wyniki oblicze
ń
wy
ś
wietlane s
ą
z
odpowiednimi symbolami:
Y
yotta
= 10
24
,
Z
zetta
= 10
21
,
E
exa
= 10
18
,
P
peta
= 10
15
,
T
tera
= 10
12
,
G
giga
= 10
9
,
M
mega
= 10
6
,
K
kilo
= 10
3
,
m
milli
= 10
– 3
,
μ
micro
= 10
– 6
,
n
nano
= 10
– 9
,
p
pico
= 10
– 12
,
f
femto
= 10
– 15
,
a
atto
= 10
– 18
,
z
zepto
= 10
– 21
,
y
yocto
= 10
– 24
Aby wej
ść
do trybu in
ż
ynierskiego, nale
ż
y nacisn
ąć
klawisze
[ MODE ] 5 ( ENG )
Aby wyj
ść
z tego trybu, nale
ż
y ponownie nacisn
ąć
klawisze [ MODE ]
5 .
¾
6 7 = 0.85714285714…
ENG
DEG
[ MODE ] 5
0
.
ENG
DEG
6
7 =
m
6 [ ] 7 [ = ]
8
5
7
.
1 4 2 8 5 7 1
4 3
ENG
DEG
μ
[ ENG ]
8 5 7 1 4 2
.
8 5 7 1 4 3
ENG
DEG
K
[ 2nd ] [
] [ 2nd ] [
] [ 2nd ]
[
]
0
.
0 0 0 8 5 7 1 4 2 8 5
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po13-
Obliczenia funkcji naukowych
Obliczenia naukowe wykonujemy w trybie MAIN ( [ MODE ] 1
( MAIN ) ) .
Logarytmy i antylogarytm
y
Logarytmy dziesi
ę
tne i naturalne i antylogarytmy obliczamy
odpowiednio za pomoc
ą
klawiszy [ log ], [ ln ], [ 2nd ] [ 10
x
] i [ 2nd ]
[ e
x
].
¾
ln 7 + log 100 = 3.94591014906
DEG
l n 7 + l o g 1 0 0 =
[ ln ] 7 [ + ] [ log ] 100 [ = ]
3
.
9 4 5 9 1 0 1 4 9 0 6
¾
10
2
+ e
–5
= 100.006737947
DEG
10
^ 2 + e ^ – 5 =
[ 2nd ] [ 10
X
] 2 [ + ] [ 2nd ] [ e
X
] 5
[ + / – ] [ = ]
1 0 0
.
0 0 6 7 3 7 9 4 7
Dzia
ł
ania na u
ł
amkach
Ulamki wy
ś
wietlane s
ą
w sposób nast
ę
puj
ą
cy :
5
」
12
Wy
ś
wietlanie
liczby
12
5
56
∪
5
」
12
Wy
ś
wietlanie
liczby
56
12
5
(Uwaga):
Je
ś
li pod czas dzia
ł
a
ń
na u
ł
amkach liczba cyfr w wyniku
(cz
ęść
ca
ł
kowita + licznik + mianownik + przecinek)
przewy
ż
sza 12, wynik zostanie automatycznie wy
ś
wietlony
w postaci u
ł
amka dziesi
ę
tnego.
Wprowadzaj
ą
c liczb
ę
mieszan
ą
, najpierw wprowad
ź
cz
ęść
ca
ł
kowit
ą
,
naci
ś
nij [ a b/c ], wprowad
ź
licznik, naci
ś
nij [ a b/c ] i wprowad
ź
mianownik.
Wprowadzaj
ą
c u
ł
amek niew
ł
a
ś
ciwy najpierw wprowad
ź
licznik, naci
ś
nij [ a b/c ] i wprowad
ź
mianownik.
¾
21
8
22
7
5
14
3
2
7
=
+
DEG
7
2
3
+ 1 4
5
7
7 [ a b/c ] 2 [ a b/c ] 3 [ + ] 14 [ a b/c ]
5 [ a b/c ] 7 [ = ]
2 2
8
2 1
.
Pod czas dzia
ł
a
ń
na u
ł
amkach nast
ę
puj
ę
automatyczne skracanie
u
ł
amka po nacisni
ę
ciu klawiszy ( [ + ], [ – ], [ x ] lub [ ] ) lub [ = ] ,
je
ś
li tylko proces ten by
ł
mo
ż
liwy.
Nacisni
ę
cie klawiszy [ 2nd ] [ d/e ]
powoduje przekszta
ł
cenie wy
ś
wietlanej warto
ś
ci w u
ł
amek
niew
ł
a
ś
ciwy lub odwrotnie.
Aby przekszta
ł
cic liczb
ę
dziesi
ę
tn
ą
na
u
ł
amek nacisnij [ a b/c ].
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po14-
¾
2
9
5
.
4
2
1
4
4
2
4
=
=
=
DEG
4
2
4
=
4 [ a b/c ] 2 [ a b/c ] 4 [ = ]
4
1
2
.
DEG
4
2
4
=
[ a b/c ]
4
.
5
DEG
4
2
4
=
[ a b/c ] [ 2nd ] [ d/e ]
9
2
.
DEG
4
2
4
=
[ 2nd ] [ d/e ]
4
1
2
.
Obliczenia zawieraj
ą
ce u
ł
amki zwyk
ł
e i dziesi
ę
tne wykonywane s
ą
w
formacie dziesi
ę
tnym.
¾
55
.
12
75
.
3
5
4
8
=
+
DEG
8
4
5
+ 3
.
7 5 =
8 [ a b/c ] 4 [ a b/c ] 5 [ + ] 3.75
[ = ]
1 2
.
5 5
Konwersja jednostek miar k
ą
tów
Kalkulator umo
ż
liwia wybieranie ró
ż
nych jednostek miar k
ą
tów:
stopni(DEG), radiany(RAD), grady(GRAD).
Trzy uk
ł
ady jednostek miar k
ą
tów zwi
ą
zane s
ą
nast
ę
puj
ą
cym
równaniem :
180
°
=
π
rad = 200 grad
1) Aby
zamie
ń
bie
żą
ce ustawienia jednostek miary k
ą
tów na
jednostki do których chcesz przeprowadzi
ć
konwersj
ę
naciskaj
klawisze [ 2nd ] [ DRG ] doputy, dopóki na ekranie nie uka
żą
si
ę
z
ą
dane jednostki.
2) Wprowad
ź
warto
ść
i naciskaj klawisze [ 2nd ] [ DRG ] doputy,
dopóki na ekranie nie uka
żą
si
ę
z
ą
dane jednostki.
¾
90 deg. = 1.57079632679 rad. = 100 grad.
DEG
[ 2nd ] [ DRG ]
0
.
RAD
9 0
O
=
90 [ 2nd ] [ DRG ]
1 .
5 7 0 7 9 6 3 2 6 7 9
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po15-
GRAD
1
.
5 7 0 7 9 6 3 2 6 7
[ 2nd ] [ DRG ]
1 0 0
.
Konwersja zapisu sze
ść
dziesi
ę
tnego do
dziesi
ę
tnego i na odwrót
Kalkulator umo
ż
liwia przekszta
ł
cenie liczb sze
ść
dziesi
ę
tnych (stopnie,
minuty, sekundy) na liczby dziesi
ę
tne i na odwrót; nale
ż
y w tym celu
nacisn
ąć
odpowiednio klawisze [
] lub [ 2nd ] [
].
Liczby sze
ść
dziesi
ę
tne wygl
ą
daj
ą
nast
ę
puj
ą
co:
125
45
׀
30
׀
׀
55
Oznacza to 125 stopni (D),
45 minut (M), 30.55 sekund(S)
(Uwaga):
Ogólna liczba miesc w cz
ęś
ciach D, M i S (z separatorami
w
łą
cznie) nie mo
ż
e przekroczy
ć
12, w przeciwnym
przypadku liczba sze
ść
dziesi
ę
tna nie mo
ż
e by
ć
wy
ś
wietlona
poprawnie.
¾
12.755 = 12
45
l
18
l l
DEG
12.755 [ 2nd ] [
]
1 2
4 5
l
1 8
l l
¾
2
45
l
10.5
l l
= 2.75291666667
DEG
2 [
] 45 [
] 10.5 [
]
2
.
7 5 2 9 1 6 6 6 6 6 7
Funkcje trygonometryczne i odwrotne
trygonometryczne
Kalkulatory
SR-281N
umo
ż
liwiaj
ą
obliczenie warto
ś
ci standardowych
funkcji trygonometrycznych i odwrotnych trygonometrycznych: sin, cos,
tan, sin
–1
, cos
–1
i tan
–1
.
(Uwaga):
Przy u
ż
ywaniu tych klawiszy upewnij si
ę
czy kalkulator jest
ustawiony na w
ł
a
ś
ciwe jednostki miary k
ą
tów.
¾
sin 30 deg.= 0.5
DEG
s i n 3 0 =
[ sin ] 30 [ = ]
0
.
5
¾
3 cos (
π
3
2
rad) = – 1.5
RAD
3
¼
c o s ( 2
¼
π
3 =
3 [ cos ] [ ( ] 2 [ x ] [ 2nd ] [
π
] [ ]
3 [ = ]
– 1
.
5
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po16-
¾
3 sin
–1
0.5 = 90 deg
DEG
3
¼
s i n
–1
0
.
5 =
3 [ 2nd ] [ sin
–1
] 0.5 [ = ]
9 0
.
Funkcje hiperboliczne i odwrotne hiperboliczne.
Kalkulatory
SR-281N
umo
ż
liwiaj
ą
obliczenie warto
ś
ci funkcji
hiperbolicznych i odwrotnych hiperbolicznych : sinh, cosh, tanh, sinh
–1
,
cosh
–1
i tanh
–1
; s
ł
u
żą
do tego klawisze [ 2nd ] [ HYP ].
(Uwaga):
Przy u
ż
ywaniu tych klawiszy upewnij si
ę
czy kalkulator jest
ustawiony na w
ł
a
ś
ciwe jednostki miary k
ą
tów.
¾
cosh 1.5 + 2 = 4.35240961524
DEG
c o s h 1
.
5 + 2 =
[ 2nd ] [ HYP ] [ cos ] 1.5 [ + ] 2 [ = ]
4
.
3 5 2 4 0 9 6 1 5 2 4
¾
sinh
–1
7 = 2.64412076106
DEG
s i n h 1
–1
7 =
[ 2nd ] [ HYP ] [ 2nd ] [ sin
–1
] 7 [ = ]
2
.
6 4 4 1 2 0 7 6 1 0 6
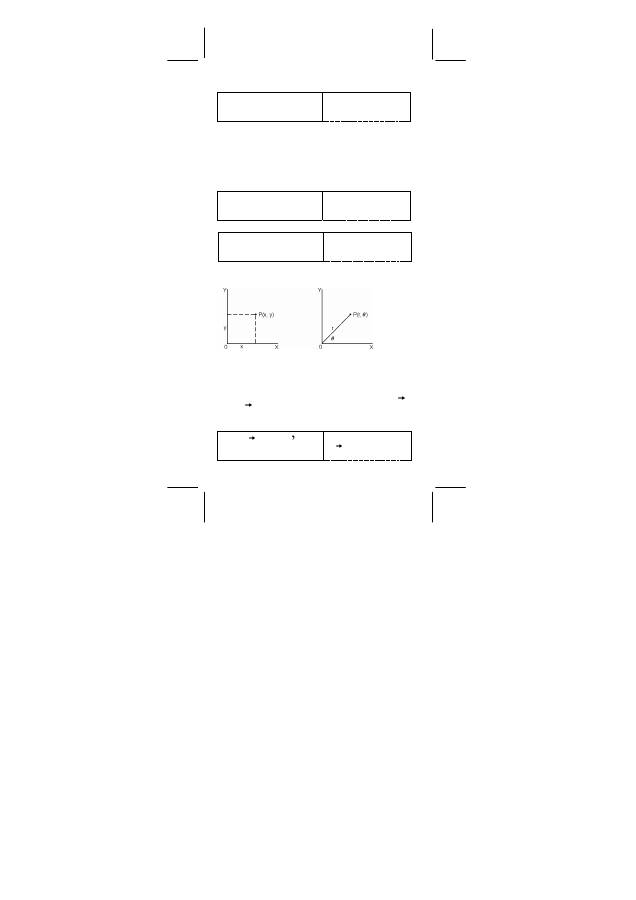
Transformacje wspó
ł
rz
ę
dnych
Uk
ł
ad prostok
ą
tny
Uk
ł
ad polarny
x + y i = r (cos
θ
+ i sin
θ
)
(Uwaga):
Przy u
ż
ywaniu tych klawiszy upewnij si
ę
czy kalkulator jest
ustawiony na w
ł
a
ś
ciwe jednostki miary k
ą
tów.
Do konwersji wspólrz
ę
dnych uk
ł
adu prostok
ą
tnego do wspólrz
ę
dnych
uk
ł
adu biegunowego i na odwrót s
ł
u
żą
klawisze [ 2nd ] [ P R ] i
[ 2nd ] [ R P ].
¾
Je
ś
li x = 5, y = 30, to jaka jest warto
ść
r,
θ
?
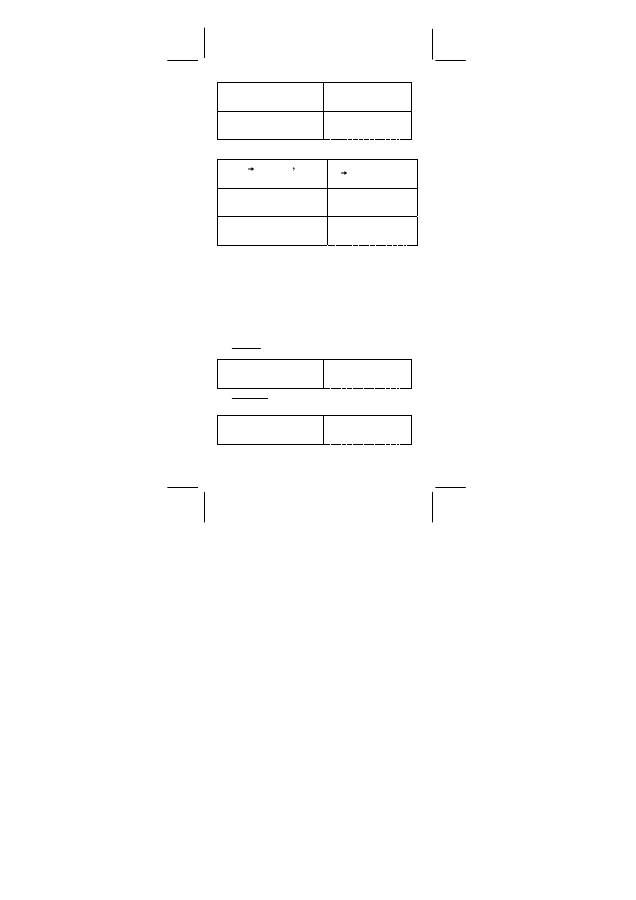
Odp :
r = 30.4138126515,
θ
= 80.537677792
o
DEG
( )
R
P ( 5
,
[ 2nd ]
[ R P ] 5 [ 2nd ] [ ] 30
3 0
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po17-
DEG
r
[ = ]
3 0
.
4 1 3 8 1 2 6 5 1 5
DEG
θ
[ 2nd ] [ X
↔
Y ]
8 0
.
5 3 7 6 7 7 7 9 2
¾
Je
ś
li r = 25,
θ
= 56
o
to jakie s
ą
warto
ś
ci x , y ?
Odp :
x = 13.9798225868, y = 20.7259393139
DEG
( )
P
R ( 2 5
,
[ 2nd ] [ P R ] 25 [ 2nd ] [ ] 56
5 6
DEG
X
[ = ]
1 3
.
9 7 9 8 2 2 5 8 6 8
DEG
Y
[ 2nd ] [ X
↔
Y ]
2 0
.
7 2 5 9 3 9 3 1 3 9
Prawdopodobi
ęń
stwo
Kalkulator umo
ż
liwia obliczenia nast
ę
puj
ą
cych funkcji
prawdopodobie
ń
stwa:
{nPr} Oblicza
ilo
ść
mo
ż
liwych permutacji n obiektów wybieranych
po r za ka
ż
dym razem.
[ nCr ] oblicza ilo
ść
mo
ż
liwych kombinacji n obiektów wybieranych
po r za ka
ż
dym razem.
[ x ! ]
Oblicza silni
ę
liczby naturalnej n , gdzie n
≦
69.
[ RND ] Generuje liczb
ę
losow
ą
w zakresie od 0.000 do 0.999
.
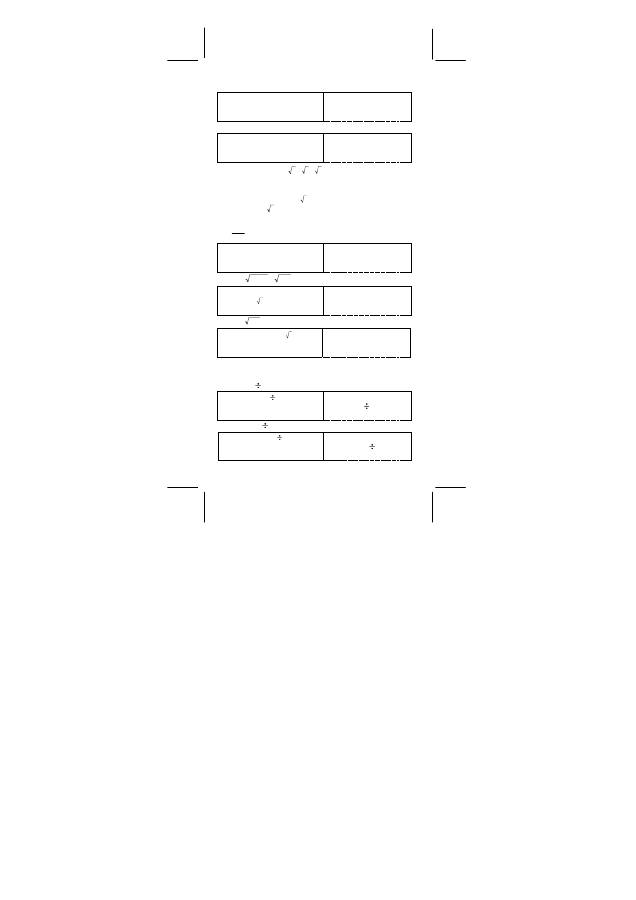
¾
840
!
]
)
4
7
(
[
!
7
=
−
DEG
7 P 4 =
7 [ 2nd ] [ nPr ] 4 [ = ]
8 4 0
.
¾
5
3
!
]
)
4
7
(
[
!
4
!
7
=
−
DEG
7 C 4 =
7 [ 2nd ] [ nCr ] 4 [ = ]
3 5
.
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po18-
¾
5 ! = 120
DEG
5 ! =
5 [ 2nd ] [ x ! ] [ = ]
1 2 0
.
¾
Generuje liczb
ę
losow
ą
w zakresie 0.000 ~ 0.999
DEG
R n d
[ 2nd ] [ RND ]
0
.
4 4 9
Inne funkcje ( 1/x, ,
3
,
X
, x
2
, x
3
, x
y
, INT, FRAC )
Kalkulator umo
ż
liwia obliczenia odwrotno
ś
ci liczby ( [ 2nd ] [ 1/x ] ),
pierwiastka kwadratowego z liczby ( [
√
] ), pierwiastka trzeciego
stopnia z liczby ( [ 2nd ] [
3
] ), pierwiastka dowolnego stopnia z
liczby ( [ 2nd ] [
X
] ), kwadratu liczby ( [ x
2
] ), sze
ś
cianu ( [ 2nd ]
[ x
3
] ), oraz funkcji wyk
ł
adniczej ( [ x
y
] ).
¾
8
.
0
.25
1
1
=
DEG
1
.
2 5
–1
=
1.25 [ 2nd ] [ 1 / x ] [ = ]
0
.
8
¾
139
=
5
+
125
+
21
+
4
+
2
3
3
2
DEG
2
2
+
√
( 4 + 2 1 ) +
2 [ x
2
] [ + ] [
√
] [ ( ] 4 [ + ] 21 [ ) ]
[ + ] [ 2nd ] [
3
] 125 [ + ] 5 [ 2nd ]
[ x
3
] [ = ]
1 3
9
.
¾
16812
=
625
+
7
4
5
DEG
7 x
y
5 + 4
X
√
6 2 5 =
7 [ x
y
] 5 [ + ] 4 [ 2nd ] [
X
] 625 [ = ]
1 6 8 1
2
.
INT
Pokazuje cz
ęść
ca
ł
kowit
ą
liczby.
FRAC
Pokazuje cz
ęść
u
ł
amkow
ą
liczby.
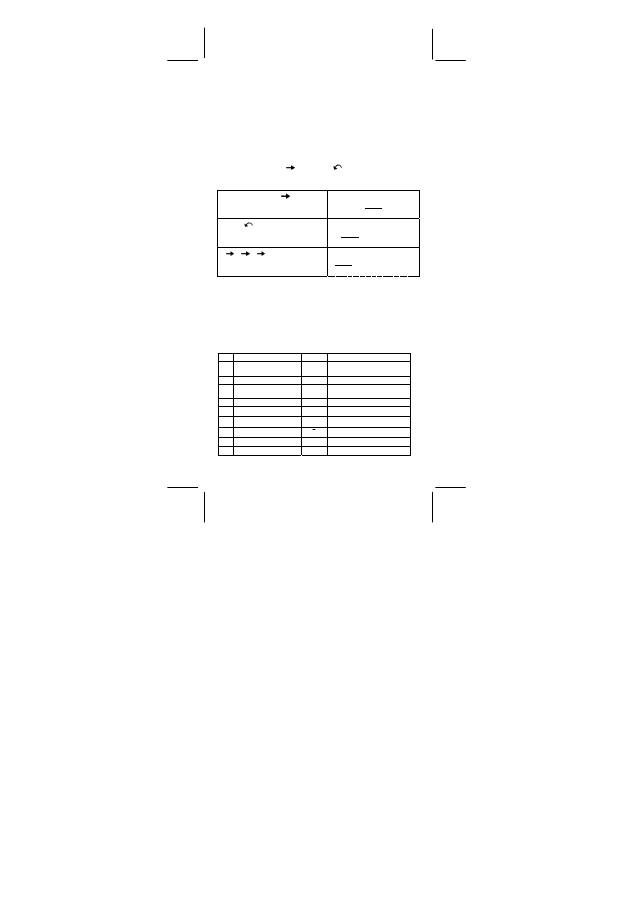
¾
INT ( 10 8 ) = INT ( 1.25 ) = 1
DEG
I N T ( 1 0
8 =
[ 2nd ] [ INT ] 10 [ ] 8 [ = ]
1
.
¾
FRAC ( 10 8 ) = FRAC ( 1.25 ) = 0.25
DEG
F R A C ( 1 0
8 =
[ 2nd ] [ FRAC ] 10 [ ] 8 [ = ]
0
.
2 5
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po19-
Konwersja jednostek
Kalkulator ma wbudowan
ą
funkcj
ę
konwersji jednostek, która
umo
ż
liwia konwersj
ę
jednostek miar.
1. Wprowad
ź
warto
ść
, któr
ą
chcesz skonwertowa
ć
.
2. Naci
ś
nij klawisz [ CONV ] aby wywola
ć
menu.
Kalkulator ma 7
menu, odpowiednio do wyboru jednostek d
ł
ugo
ś
ci, powierzchni,
temperatury, obj
ę
to
ś
ci, masy, energii oraz ci
ś
nienia.
3. Zmieniaj list
ę
jednostek naciskaj
ą
c klawisz [ CONV ] dopóki w
menu nie uka
ż
e jednostka, której szukasz, a nast
ę
pnie naci
ś
nij
klawisz [ = ].
4. Wci
ś
ni
ę
cie klawiszy [
] lub [ 2nd ] [
] spowoduje
skonwertowanie warto
ś
ci do innego uk
ł
adu.
¾
1 y d
2
= 9 f t
2
= 0.00000083612 km
2
DEG
f t
2
y d
2
m
2
1 [ CONV ] [ CONV ] [
] [ = ]
1
.
DEG
f t
2
y d
2
m
2
[ 2nd ] [
]
9
.
DEG
k m
2
h e c t a r e s
[
] [
] [
]
0
.
0 0 0 0 0 0 8 3 6 1 2
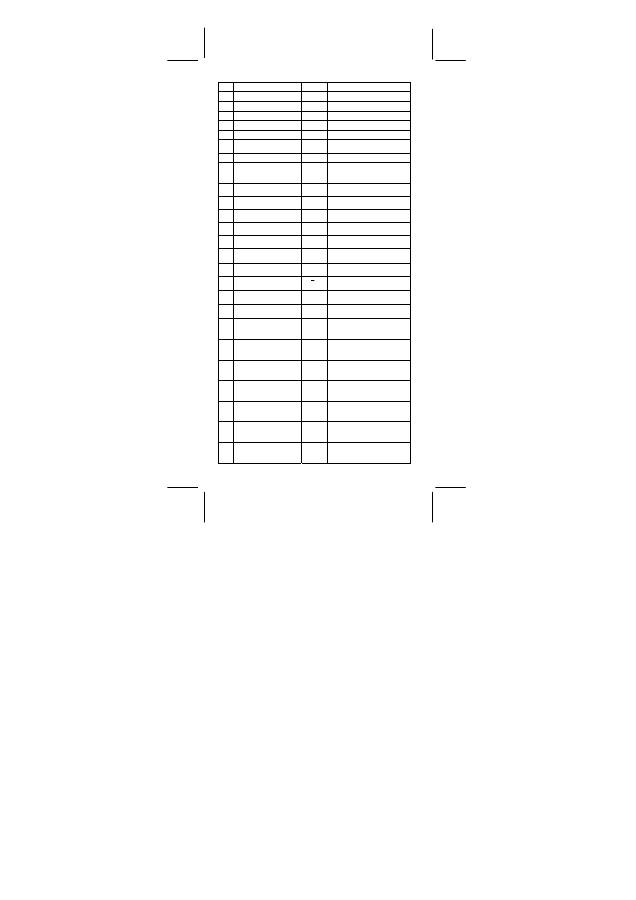
Sta
ł
e fizyczne
Kalkulator pozwala w obliczeniach u
ż
y
ć
136 sta
ł
ych fizycznych.
Sta
ł
e
fizyczne:
Dane cytowane s
ą
zgodnie z: Peter J.Mohr and Barry N.Taylor,
CODATA Recommended Values of the Fundamental Physical
Constants:1998, Journal of Physical and Chemical Reference
Data,Vol.28, No.6,1999 oraz Reviews of Modern Physics,Vol.72, No.2,
2000.
No.
Sta
ł
a Symbol
Warto
ść
, jednostki
1.
Pr
ę
dko
ść
ś
wiat
ł
a w
pró
ż
ni
c
299792458 m s
–1
2. Sta
ł
a magnetyczna
μ
0
1.2566370614 x10
–6
N A
–2
3.
Przenikalno
ść
elektryczna
pró
ż
ni
ε
0
8.854187817 x 10
–12
F m
–1
4.
Impedancja pró
ż
ni
Z
0
376.730313461
Ω
5. Sta
ł
a grawitacji Newtona
G
6.67310 x10
–11
m
3
kg
–1
s
–2
6. Sta
ł
a Plancka
h
6.6260687652 x10
–34
J s
7.
Sta
ł
a Plancka /2pi
h
1.05457159682 x10
–34
J s
8. Sta
ł
a Awogadra
N
A
6.0221419947 x10
23
mol
–1
9. D
ł
ugo
ść
Plancka
lp
1.616012 x10
–35
m

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po20-
10. Czas
Plancka
tp
5.390640 x10
–44
s
11. Masa
Plancka
mp
2.176716 x10
–8
kg
12.
Jednostka masy
atomowej
m
μ
1.6605387313 x10
–27
kg
13.
Równowa
ż
nik
energetyczny jednostki
masy atomowej
m
μ
c
2
1.4924177812 x10
–10
J
14.
Stala Faraday'a
IF
96485.341539 C mol
–1
15.
Ladunek elementarny
e 1.60217646263
x10
–19
C
16. Stosunek eV/J
eV 1.60217646263
x10
–19
J
17.
Ladunek elementarny
e/h 2.41798949195
x10
14
AJ
–1
18. Molowa sta
ł
a gazowa
R
8.31447215 J mol
–1
K
–1
19.
Sta
ł
a Boltzmanna
k 1.380650324
x10
–23
J K
–1
20. Sta
ł
a molowa Plancka
N
A
h 3.99031268930x10
–10
Js mol
–1
21.
Stala Sackura–Tetrode
entropii bezwzgl
ę
dnej
S
0
/R
–
1.164867844
22. Sta
ł
a przesuni
ęć
Wiena
b 2.897768651
x10
–3
m K
23.
Parametr siatki
krystalicznej krzemu
a 543.10208816
x10
–12
m
24.
Sta
ł
a Stefana-
Boltzmanna
σ
5.67040040 x10
–8
W m
–2
K
–4
25.
Standardowe
przy
ś
pieszenie
grawitacyjne
g
9.80665 m s
–2
26. Masa
atomowej,
kg
μ
1.6605387313 x10
–27
kg
27.
Pierwsza sta
ł
a
promieniowania
c
1
3.7417710729 x10
–16
Wm
2
28.
Pierwsza sta
ł
a
promieniowania dla
spektralnej
ś
wiat
ł
o
ś
ci
c
1
L
1.19104272293x10
–16
Wm
2
sr
–1
29.
Druga sta
ł
a
promieniowania
c
2
1.438775225 x10
–2
m K
30.
Objetosc molarna gazu
idealnego
Vm
22.41399639 x10
–3
m
3
mol
–1
31. Sta
ł
a Rydberga
R
∞
10973731.5685 m
–1
32. Sta
ł
a Rydberga, Hz
R
∞
c
3.28984196037 x10
15
Hz
33. Sta
ł
a Rydberga, J
R
∞
hc
2.1798719017 x10
–18
J
34. Energia
Hartree
E
h
4.3597438134 x10
–18
J
35. Kwant
cyrkulacji
h/me
7.27389503253 x10
–4
m
2
s
–1
36. Sta
ł
a struktury subtelnej
α
7.29735253327 x10
–3
37. Sta
ł
a Loschmidta
n
0
2.686777547
x10
25
m
–3
38. Promien Bohra
a
0
0.52917720832
x10
–10
m
39.
Kwant strumienia
magnetycznego
Φ
0
2.06783363681 x10
–15
Wb
40. Kwant przewodno
ś
ci
G
0
7.74809169628
x10
–5
S
41.
Odwrotno
ść
kwantu
przewodno
ś
ci
G
0
–1
12906.4037865
Ω
42. Sta
ł
a Josephsona
KJ
483597.89819 x10
9
Hz V
–1
43. Sta
ł
a von Klitzinga
RK
25812.8075730
Ω
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po21-
44. Magneton
Bohra
μ
B
927.40089937 x10
–26
J T
–1
45. Magneton Bohra w Hz/T
μ
B/h
13.9962462456 x10
9
Hz T
–1
46. Magneton Bohra w K/T
μ
B/k
0.671713112 K T
–1
47. Magneton
j
ą
drowy
μ
N
5.0507831720 x10
–27
J T
–1
48.
Magneton j
ą
drowy, MHz/T
μ
N/h
7.6225939631 MHz T
–1
49. Magneton
j
ą
drowy, K/T
μ
N/k
3.658263864 x10
–4
K T
–1
50.
Klasyczny promie
ń
elektronu
re
2.81794028531 x10
–15
m
51. Masa
elektronu
me
9.1093818872 x10
–31
kg
52.
Równowa
ż
nik
energetyczny masy
elektronu
mec
2
8.1871041464 x10
–14
J
53.
Stosunek masy elektronu do
masy mionu
me/m
μ
4.8363321015 x10
–3
54.
Stosunek masy elektronu do
masy taonu
me/m
τ
2.8755547 x10
–4
55.
Stosunek masy elektronu do
masy protonu
me/mp
5.44617023212 x10
–4
56.
Stosunek masy elektronu do
masy neutronu
me/mn
5.43867346212 x10
–4
57.
Stosunek masy elektronu do
masy deuteronu
me/md
2.72443711706x10
–4
58.
Stosunek
ł
adunku
elektronu do jego masy
–
e/me
–
1.75882017471 x10
11
Ckg
–1
59.
Comptonowska d
ł
ugo
ść
fali
λ
c
2.42631021518 x10
–12
m
60.
Comptonowska d
ł
ugo
ść
fali /2pi
λ
c
386.159264228 x10
–15
m
61.
Przekrój czynny
Thomsona
σ
e
0.66524585415 x10
–28
m
2
62.
Magnetyczny moment
elektronu
μ
e
–
928.47636237x10
–26
J T
–1
63.
Stosunek momentu
magnetycznego do
magnetonu Bohra
μ
e/
μ
B
–
1.00115965219
64.
Stosunek momentu
magnetycznego do
magnetonu j
ą
drowego
μ
e/
μ
N
–
1838.28196604
65.
Stosunek momentów
magnetycznych elektronu
i mionu
μ
e/
μ
μ
206.766972063
66.
Stosunek momentów
magnetycznych elektronu
i protonu
μ
e/
μ
p
–
658.210687566
67.
Stosunek momentów
magnetycznych elektronu
i neutronu
μ
e/
μ
n
960.9205023
68.
Stosunek momentów
magnetycznych elektronu
i deuteronu
μ
e/
μ
d
–
2143.92349823
69.
Stosunek momentów
magnetycznych elektronu
i ekranowanego helionu
μ
e/
μ
'h
864.05825510
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po22-
70.
Anomalia momentu
magnetycznego elektronu
a e
1.15965218694 x10
–3
71. Czynnik
g
elektronu
g e
–
2.00231930437
72.
Wspó
ł
czynnik
giromagnetyczny
elektronu
γ
e
1.76085979471 x10
11
s
–1
T
–1
73. Masa
mionu
m
μ
1.8835310916 x10
–28
kg
74.
Równowa
ż
nik
energetyczny masy
mionu
m
μ
c
2
1.6928333214 x10
–11
J
75.
Stosunek mas mionu i
taonu
m
μ
/m
τ
5.9457297 x10
–2
76.
Stosunek mas mionu i
protonu
m
μ
/mp
0.11260951733
77.
Stosunek mas mionu i
neutronu
m
μ
/mn
0.11245450793
78.
Anomalia momentu
magnetyczego mionu
a
μ
1.1659160264 x10
–3
79. Czynnik
g
mionu
g
μ
–
2.00233183201
80.
Comptonowska d
ł
ugo
ść
fali mionu
λ
c,
μ
11.7344419735 x10
–15
m
81.
Comptonowska d
ł
ugo
ść
fali mionu /2pi
λ
c,
μ
1.86759444455 x10
–15
m
82.
Magnetyczny moment
mionu
μ
μ
–
4.4904481322x10
–26
J T
–1
83.
Stosunek momentu
magnetycznego mionu i
magnetonu Bohra
μ
μ
/
μ
B
–
4.8419708515 x10
–3
84.
Stosunek momentu
magnetycznego mionu i
magnetonu j
ą
drowego
μ
μ
/
μ
N
–
8.8905977027
85.
Stosunek momentu
magnetycznego mionu i
protonu
μ
μ
/
μ
p
–
3.1833453910
86.
Comptonowska d
ł
ugo
ść
fali taonu
λ
c,
τ
0.6977011 x10
–15
m
87.
Comptonowska d
ł
ugo
ść
fali taonu /2pi
λ
c,
τ
0.11104218 x10
–15
m
88. Masa taonu
m
τ
3.1678852 x10
–27
kg
89.
Równowa
ż
nik
energetyczny masy taonu
m
τ
c
2
2.8471546 x10
–10
J
90.
Stosunek mas taonu i
protonu
m
τ
/mp
1.8939631
91.
Comptonowska d
ł
ugo
ść
fali protonu
λ
c,p
1.32140984710 x10
–15
m
92.
Comptonowska d
ł
ugo
ść
fali protonu /2pi
λ
c,p
0.21030890892 x10
–15
m
93. Masa
protonu
mp
1.6726215813 x10
–27
kg
94.
Równowa
ż
nik
energetyczny masy
protonu
mpc
2
1.5032773112 x10
–10
J
95.
Stosunek mas protonu i
neutronu
mp/mn
0.99862347856
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po23-
96.
Stosunek
ł
adunku
protonu do jego masy
e/mp
9.5788340838 x10
7
C kg
–1
97.
Moment magnetyczny
protonu
μ
p
1.41060663358 x10
–26
J T
–1
98.
Moment magnetyczny
ekranowanego protonu
μ
'p
1.41057039959 x10
–26
J T
–1
99.
Stosunek momentu
magnetycznego protonu
do magnetonu j
ą
drowego
μ
p/
μ
N
2.79284733729
100.
Stosunek momentów
magnetycznych protonu i
neutronu
μ
p/
μ
n
–
1.4598980534
101.
Stosunek momentów
magnetycznych
ekranowanego protonu i
magnetonu Bohra
μ
'p/
μ
B
1.52099313216 x10
–3
102.
Wspó
ł
czynnik
giromagnetyczny protonu
γ
p
2.6752221211 x10
8
s
–1
T
–1
103.
Wspó
ł
czynnik
giromagnetyczny
ekranowanego protonu
γ
'p
2.6751534111 x10
8
s
–1
T
–1
104.
Poprawka na
ekranowanie
magnetyczne protonu
σ
'p
25.68715 x10
–6
105. Czynnik
g
protonu
g p
5.58569467557
106.
Comptonowska d
ł
ugo
ść
fali neutronu
λ
c,n
1.31959089810 x10
–15
m
107.
Comptonowska d
ł
ugo
ść
fali neutronu /2pi
λ
c,n
0.21001941422 x10
–15
m
108. Masa neutronu
mn
1.6749271613 x10
–27
kg
109.
Równowa
ż
nik
energetyczny masy
neutronu
mnc
2
1.5053494612 x10
–10
J
110.
Magnetyczny moment
neutronu
μ
n
–
0.9662364023x10
–26
J T
–1
111.
Stosunek momentu
magnetycznego neutronu
do magnetonu Bohra
μ
n/
μ
B
–1.0418756325 x10
–3
112. Czynnik
g
neutronu
gn
–
3.8260854590
113.
Wspó
ł
czynnik
giromagnetyczny
neutronu
γ
n
1.8324718844 x10
8
s
–1
T
–1
114.
Masa deuteronu
md
3.3435830926 x10
–27
kg
115.
Równowa
ż
nik
energetyczny masy
deuteronu
mdc
2
3.0050626224 x10
–10
J
116. Masa molowa deuteronu
M(d) 2.01355321271x10
–3
kg
mol
–1
117.
Stosunek mas deuteronu
i elektronu
md/me
3670.48295508
118.
Stosunek mas deuteronu
i protonu
md/mp
1.99900750083
119.
Moment magnetyczny
deuteronu
μ
d
0.43307345718 x10
–26
J T
–1
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po24-
120.
Stosunek momentu
magnetycznego
deuteronu do magnetonu
Bohra
μ
d/
μ
B
0.46697545565 x10
–3
121.
Stosunek momentu
magnetycznego
deuteronu do magnetonu
j
ą
drowego
μ
d/
μ
N
0.85743822849
122.
Stosunek momentów
magnetycznych
deuteronu i protonu
μ
d/
μ
p
0.30701220835
123. Masa helionu
mh
5.0064117439 x10
–27
kg
124.
Równowa
ż
nik
energetyczny masy
helionu
mhc
2
4.4995384835 x10
–10
J
125. Masa molowa helionu
M(h) 3.01493223470x10
–3
kg mol
–1
126.
Stosunek mas helionu i
elektronu
mh/me
5495.88523812
127.
Stosunek mas helionu i
protonu
mh/mp
2.99315265851
128.
Moment magnetyczny
ekranowanego helionu
μ
'h
–
1.07455296745 x10
–26
J T
–1
129.
Stosunek momentu
magnetyczego
ekranowanego helionu do
magnetonu Bohra
μ
'h/
μ
B
–
1.15867147414 x10
–3
130.
Stosunek momentu
magnetyczego
ekranowanego helionu do
magnetonu j
ą
drowego
μ
'h/
μ
N
–
2.12749771825
131.
Wspó
ł
czynnik
giromagnetyczny
ekranowanego helionu
γ
'h
2.03789476485 x10
8
s
–1
T
–1
132. Masa cz
ą
stki alfa
m
α
6.6446559852 x10
–27
kg
133.
Równowa
ż
nik energii
cz
ą
stki alfa
m
α
c
2
5.9719189747 x10
–10
J
134. Masa molowa cz
ą
stki alfa
M(
α
)
4.00150617471 x10
–3
kg
mol
–1
135.
Stosunek mas cz
ą
stki alfa
i elektronu
m
α
/me
7294.29950816
136.
Stosunek mas cz
ą
stki alfa
i protonu
m
α
/mp
3.97259968461
Aby wstawi
ć
sta
łą
w pozycji gdzie znajduje si
ę
kursor:
1. Naci
ś
nij [ CONST ] aby wy
ś
wietli
ć
menu sta
ł
ych fizycznych.
2. Naciskaj [
] lub [ 2nd ] [
] dopóki sta
ł
a któr
ą
chcesz wstawi
ć
nie zostanie podkre
ś
lona.
3. Naci
ś
nij [ = ].
Aby wstawi
ć
sta
łą
fizyczn
ą
, mo
ż
esz tak
ż
e klawisz [ CONST ] i liczb
ę
od 1 do 136.
Na przyk
ł
ad, naci
ś
nij 15 [ CONST ].
DEG
e
1
.
6 0 2 1 7 6 4 6 2 6 3
–19
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po25-
¾
3 x N
A
= 1.80664259841 x 10
24
CONST DEG
h
h
N
A
l p
t p
3 [ x ] [ CONST ] [ CONST ] [
]
[
]
6
.
0 2 2 1 4 1 9 9 4 7
23
CONST DEG
0 0 8
:
m o l
–1
[ = ]
6
.
0 2 2 1 4 1 9 9 4 7
23
CONST DEG
3
¼
N
A
=
[ = ] [ = ]
1
.
8 0 6 6 4 2 5 9 8 4 1
24
Obliczenia w trybie Base–n
Obliczenia Base-n wykona
ć
mo
ż
na w trybie MAIN ( [ MODE ] 1
( MAIN ) ).
Kalkulator umo
ż
liwia obliczenia w uk
ł
adach liczbowych innych ni
ż
dziesi
ę
tne.
Mo
ż
esz tak
ż
e dodawa
ć
, odeimowa
ć
, mno
ż
y
ć
i dzieli
ć
liczby w uk
ł
adach dwójkowym, ósemkowym i szestnastkowym.
Poni
ż
ej podane s
ą
liczby, na których mo
ż
na dokonywa
ć
oblicze
ń
w
odpowiednich systemach liczbowych.
Uk
ł
ad dwójkowy ( b) :
0, 1
Uk
ł
ad ósemkowy ( o ) :
0, 1, 2, 3, 4, 5, 6, 7
Uk
ł
ad dziesi
ę
tny :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Uk
ł
ad szestnastkowy ( h ) :
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Wygl
ą
d cyfr literowych A, B, C, D, E i F w uk
ł
adzie szestnastkowym
jest odmienny od zwyk
ł
ych liter.
Klawisz
Ekran
(górny)
Ekran
(dolny)
Klawisz
Ekran
(górny)
Ekran
(dolny)
A /A
D ID
B IB
E IE
C
I
C
F IF
Wybór
żą
danego uk
ł
adu liczbowego przeprowadzamy za pomoc
ą
klawiszy [ BIN ], [ OCT ], [ DEC ], [ HEX ].
Wska
ź
niki " BIN ", " b ",
" OCT ", " o ", " HEX ", " h " pokazuj
ą
, jakiego uk
ł
adu u
ż
ywasz.
Je
ś
li
na ekranie nie ma
ż
adnych wska
ź
ników, oznacza to
ż
e wybrany jest
uk
ł
ad dziesi
ę
tny.

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po26-
Konwersja liczb
¾
37 (base 8) = 31 (base 10) = 1F (base 16)
DEG
OCT
[ 2nd ] [ OCT ] 37
0 0 0 0 0 0 0 0 0 3 7
o
DEG
[ 2nd ] [ DEC ]
3 1
.
DEG
HEX
[ 2nd ] [ HEX ]
0 0 0 0 0 0 1 F
h
Funkcja bloków
Wynik oblicze
ń
w uk
ł
adzie dwójkowym wy
ś
wietlany b
ę
dzie za pomoc
ą
funkcji bloków.
Liczba o maksymalnej d
ł
ugo
ś
ci 32 cyfr wy
ś
wietlana
jest w postaci 4 bloków po 8 cyfr.
1 1 0 1 00 11 b
DEG BIN
Ogó
ł
em bloków 4
Wy
ś
wietlony jest blok 1
Wy
ś
wietlony jest blok 2
Wy
ś
wietlony jest blok 3
Wy
ś
wietlony jest blok 4
Ogó
ł
em bloków 3
Ogó
ł
em bloków 2
Ogó
ł
em bloków 1
Ka
ż
dy blok sk
ł
ada si
ę
z górnej i dolnej cz
ę
sci.
W cz
ęś
ci gornej
pokazana pozycja bloku, w cz
ęś
ci dolnej pokazano, z ilu bloków
sk
ł
ada si
ę
wynik.
W uk
ł
adzie dwójkowym blok 1 wy
ś
wietla si
ę
bezpo
ś
rednio po
zako
ń
czeniu oblicze
ń
.
Inne bloki (2 – 4) mo
ż
na wy
ś
wietli
ć
naciskaj
ą
c
klawisz [
].
Wprowad
ź
my, na przyk
ł
ad, liczb
ę
47577557
16
Naciskamy [ 2nd ] [ HEX ] 47577557
ś
ó
[ 2nd ] [ BIN ]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Wy
ś
wietlony Blok 1

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po27-
[
]
0 1 1 1 0 1 0 1
b
DEG BIN
–
–
Wy
ś
wietl ony Bl ok 2
[
]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Wy
ś
w ietlony Blok 3
[
]
0 1 0 0 0 1 1 1
b
DEG BIN
– – –
Wy
ś
wietlony Blok 4
47577557
16
= Blok 4 + Blok 3 + Blok 2 + Blok 1
= 01000111010101110111010101010111
2
Operacje arytmetyczne w róznych uk
ł
adach
¾
1IEIF
16
+ 1234
10
1001
2
= 1170
8
DEG
OCT
h 1 IE IF + 1 2 3 4
b 1
[ 2nd ] [ HEX ] 1E F [ + ] [ 2nd ]
[ DEC ] 1234 [ ] [ 2nd ] [ BIN ] 1001
[ = ] [ 2nd ] [ OCT ]
0 0 0 0 0 0 0 1 1 7 0
o
Warto
ś
ci ujemne
W ukladach dwójkowym, ósemkowym i szestnastkowym warto
ś
ci
ujemne reprezentowane s
ą
przy pomocy komplementu.
Komplement
to wynik odejmowania liczby od
100000000000000000000000000000000 w uk
ł
adach innych, ni
ż
dziesi
ę
tny, otrzymywany naci
ś
ni
ę
ciem klawisza [ NEG ] .
¾
3/A
16
= NEG IFIFIFIFIFIFIC6
16
DEG
HEX
N E G
h 3 /A
[ 2nd ] [ HEX ] 3 A [ NEG ]
F F F F F F C 6
h
Operacje logiczne
Operacje logiczne wykonywane s
ą
przy pomocy operatorów
logicznych (AND), negacji logicznej (NAND), sumy logicznej (OR),
ekskluzywnej sumy logicznej (XOR), negacji (NOT) i negacji
ekskluzywnej sumy logicznej (XNOR).
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po28-
¾
1010
2
AND ( /A
16
OR 7
16
) = 12
8
DEG
OCT
b 1 0 1 0
A N D
( h
[ 2nd ] [ BIN ] 1010 [ AND ] [ ( ] [ 2nd ]
[ HEX ] A [ OR ] 7 [ ) ] [ = ] [ 2nd ]
[ OCT ]
0 0 0 0 0 0 0 0 0 1 2
o
Obliczenia
statystyczne
Obliczenia statystyczne dokonywane s
ą
w trybie STAT ( [ MODE ] 2
( STAT ) ).
W trybie oblicze
ń
statystycznych mo
ż
na dokonywa
ć
oblicze
ń
z jedn
ą
lub dwiema zmiennymi.
Aby wej
ść
do trybu STATP, naci
ś
nij klawisze [ MODE ] 2 ( STAT ).
W
menu STAT s
ą
sz
ęść
opcji, wybierz jedn
ą
z nich.
DEG
1–VAR LIN LOG
STAT
[
] [
] [
]
DEG
EXP PWR D–CL
STAT
Obliczenia statystyczne z jedn
ą
zmienn
ą
1–VAR
Obliczenia statystyczne z jedn
ą
zmienn
ą
Obliczenia z dwiema zmiennymi i obliczenia regresji
LIN
Regresja liniowa
y = a + b x
LOG
Regresja logarytmiczna y = a + b lnx
EXP Regresja
wyk
ł
adnicza
y = a • e
bx
POW Regresja
pot
ę
gowa
y = a • x
b
D–CL
Wyczyszczenie wszystkich danych statystycznych
Wprowadzenie danych
Przed rozpocz
ę
ciem oblicze
ń
statystycznych nale
ż
y si
ę
upewni
ć
,
ż
e
poprzednio wprowadzone dane zosta
ł
y wyczyczone ( D–CL ).
(A) Aby wprowadzi
ć
dane statystyczne dla oblicze
ń
z jedn
ą
zmienn
ą
:
# Dane
indywidualne
:
[ DATA ] < warto
ść
x >
# Warto
ść
wielokrotnie powtórzona:
[ DATA ] <warto
ść
x > [ x ] < liczba powtórze
ń
>
(B) Aby wprowadzi
ć
dane statystyczne dla oblicze
ń
z dwiema
zmiennymi i oblicze
ń
regresji:
# Zbiór danych :
[ DATA ] < warto
ść
x > [ ] < warto
ść
y >
# Warto
ść
wielokrotnie powtórzona :
[ DATA ] < warto
ść
x > [ ] < warto
ść
y > [ x ] < liczba
powtórze
ń
>
(Uwaga): Nawet je
ś
li wyjdziesz z trybu STAT, wszystkie wprowadzone
dane pozostan
ą
w pami
ę
ci, dopóki nie naci
ś
niesz D-CL.
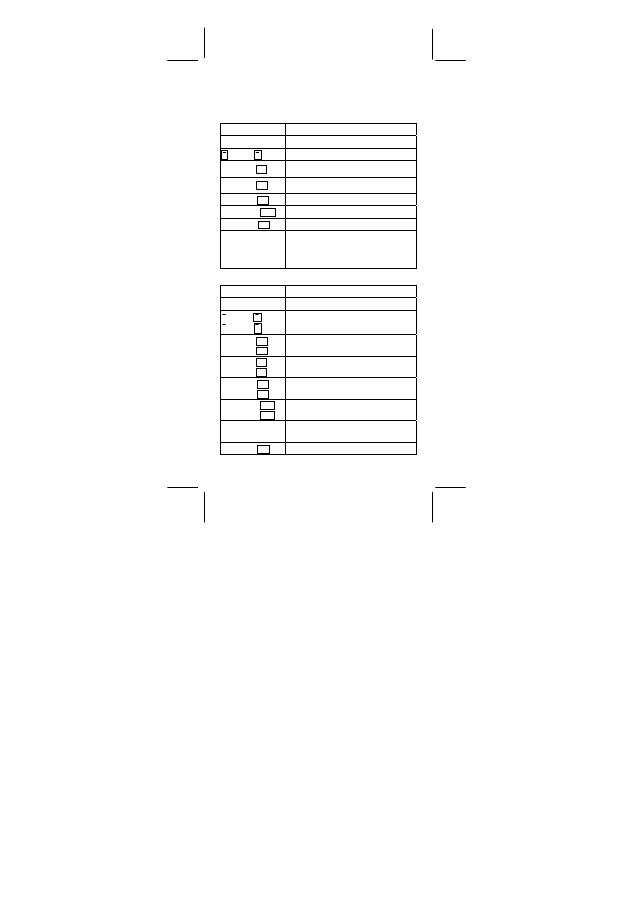
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po29-
Wy
ś
wietlanie wyników
Wynik oblicze
ń
statystycznych zale
ż
y od wprowadzonych danych.
Oblicze
ń
mo
ż
na dokona
ć
, naciskaj
ą
c klawisze, jak pokazano w tabeli.
Obliczenia statystyczne z jedn
ą
zmienn
ą
Zmienne Znaczenie
n ( [ n ] )
Liczba wprowadzonych warto
ś
ci x
x
( [2nd]+[
x
] )
Ś
rednia wszystkich warto
ś
ci x
Sx
( [2nd]+[
Sx
] )
Odchylenie standardowe próbki dla warto
ś
ci
x
σ
x
( [2nd]+[
σ
x
] )
Odchylenie standardowe populacji dla
warto
ś
ci x
∑
x
( [2nd]+[
∑
x
] )
Suma wszystkich warto
ś
ci x
∑
x
2
( [2nd]+[
∑
x
2
]) Suma wszystkich warto
ś
ci x
2
CP
( [2nd]+[
CP
] )
Poziom istotno
ś
ci testu warto
ś
ci x
CPK ( [CPK] )
Minimalne (CPU, CPL) warto
ś
ci x, gdzie
CPU to zadana granica górna poziomu
istotno
ś
ci testu, a CPL to zadana granica
dolna poziomu istotno
ś
ci testu
CPK = Min ( CPU , CPL ) = CP ( 1 – Ca )
Obliczenia statystyczne z dwiema zmiennymi i obliczenia regresji
Zmienne Znaczenie
n ( [ n ] )
Liczba wprowadzonych par x-y
x
( [2nd]+[
x
] )
y
( [2nd]+[
y
] )
Ś
rednia warto
ś
ci x lub y
Sx
( [2nd]+[ Sx ] )
Sy
( [2nd]+[ Sy ] )
Odchylenie standardowe warto
ś
ci x lub y
próbki
σ
x
( [2nd]+[
σ
x
] )
σ
y
( [2nd]+[
σ
y
] )
Odchylenie standardowe w populacji
warto
ś
ci x lub y
∑
x
( [2nd]+[
∑
x
] )
∑
y
( [2nd]+[
∑
y
] )
Suma warto
ś
ci wszystkich x lub y
∑
x
2
( [2nd]+[
∑
x
2
])
∑
y
2
( [2nd]+[
∑
y
2
])
Suma warto
ś
ci wszystkich x
2
lub y
2
∑
x y
Suma warto
ś
ci ( x • y ) dla wszystkich par x-
y
CP
( [2nd]+[
CP
] )
Poziom istotno
ś
ci testu warto
ś
ci x
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po30-
CPK ( [ CPK ] )
Minimalne (CPU, CPL) warto
ś
ci x, gdzie
CPU to zadana granica górna poziomu
istotno
ś
ci testu, a CPL to zadana granica
dolna poziomu istotno
ś
ci testu
CPK = Min ( CPU , CPL ) = CP ( 1 – Ca )
a ( [2nd]+[
a ] )
Sta
ł
a a regresji
b ( [2nd]+[
b ] )
Sta
ł
a b regresji
r ( [2nd]+[
r ] )
Wspó
ł
czynnik korelacji r
x
’
([ x
’
] )
Przewidywana warto
ść
x
y
’
([ y
’
] )
Przewidywana warto
ść
y
Mo
ż
esz wprowadzi
ć
dodatkowo nowe dane w dowolnej chwili.
Kalkulator automatycznie przelicza statystyk
ę
po ka
ż
dym naci
ś
ni
ę
ciu
klawisza [ DATA ] i wprowadzeniu nowych danych.
¾
Wprowad
ź
dane :
USL
= 95, LSL = 70, DATA 1 = 75, DATA 2 = 85,
DATA 3 = 90, DATA 4 = 82, DATA 5 = 77, i oblicz n = 5, = 81.8,
Sx = 6.05805249234,
σ
x = 5.41848687366, CP = 0.76897236513,
i CPK = 0.72590991268
DEG
STAT
1–
V A R
L I N
L O G
[ MODE ] 2
DEG
STAT
D A T A
5
[ = ] [ DATA ] 75 [ DATA ] 85 [ DATA ] 90
[ DATA ] 82 [ DATA ] 77
7 7
DEG
STAT
n
[ n ]
5
.
DEG
STAT
x
[ 2nd ] [ x
]
8 1
.
8
DEG
STAT
S x
[ 2nd ] [ Sx ]
6
.
0 5 8 0 5 2 4 9 2 3 4
DEG
STAT
σ
x
[ 2nd ] [
σ
x ]
5
.
4 1 8 4 8 6 8 7 3 6 6
DEG
STAT
U S L =
[ 2nd ] [ CP
] 95
9 5
CP
USL
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po31-
DEG
STAT
L S L =
[ = ] 70
7 0
CP
LSL
DEG
STAT
C P
[ = ]
0
.
7 6 8 9 7 2 3 6 5 1 3
DEG
STAT
U S L =
[ CPK ]
9 5
.
CPK
USL
DEG
STAT
L S L =
[ = ]
7 0
.
CPK
LSL
DEG
STAT
C P K
[ = ]
0
.
7 2 5 9 0 9 9 1 2 6 8
¾
Oblicz sta
ł
e a, b i r regresji liniowej dla poni
ż
szych danych i oblicz
x = ? .
dla y =573 i y = ?
dla x = 19.
Dane 15 17 21 28
FREQ. 451 475 525 678
DEG
STAT
1–
V A R
L I N
L O G
[ MODE ] 2 [
]
DEG
STAT
D A T A
4 = 2 8
,
[ = ] [ DATA ] 15 [ ] 451 [ DATA ] 17
[ ] 475 [ DATA ] 21 [ ] 525 [ DATA ]
28 [ ] 678
6 7 8
REG
DEG
STAT
a
[ 2nd ] [ a ]
1 7 6
.
1 0 6 3 2 9 1 1 4
REG
DEG
STAT
b
[ 2nd ] [ b ]
1 7
.
5 8 7 3 4 1 7 7 2 2
REG
DEG
STAT
r
[ 2nd ] [ r ]
0
.
9 8 9 8 4 5 1 6 4 1 3
REG
DEG
STAT
x
’
5 7 3
573 [ x
’
]
2 2
.
5 6 7 0 0 7 3 4 1 3
REG

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po32-
DEG
STAT
y
’
1 9
19 [ y
’
]
5 1 0
.
2 6 5 8 2 2 7 8 5
REG
Kasowanie danych
Sposób kasowania danych zale
ż
y od tego, czy zostal naci
ś
ni
ę
ty
klawisz [ DATA ].
Aby wykasowa
ć
wprowadzone dane, je
ś
li klawisz [ DATA ] nie zosta
ł
naic
ś
ni
ę
ty, po prostu naci
ś
nij [ CE ].
Aby wykasowa
ć
dane zapisane do pami
ę
ci naci
ś
ni
ę
ciem klawisza
[ DATA ] ,
(A) Aby wykasowa
ć
dane statystyczne dla oblicze
ń
z jedn
ą
zmienn
ą
:
# <warto
ść
x > [ 2nd ] [ DEL ]
# <
warto
ść
x > [ x ] < liczba powtórze
ń
> [ 2nd ] [ DEL ]
(B) Aby wykasowa
ć
dane statystyczne dla oblicze
ń
z dwiema
zmiennymi i oblicze
ń
regresji :
# Zbiór danych :
< warto
ść
x > [ ] < warto
ść
y > [ 2nd ] [ DEL ]
# Warto
ść
wielokrotnie powtórzona :
< warto
ść
x > [ ] < warto
ść
y > [ x ] < liczba powtórze
ń
> [ 2nd ]
[ DEL ]
Je
ś
li wprowadzile
ś
i kasujesz warto
ść
, omy
ł
kowo nie dopisan
ą
do
danych w pami
ę
ci, wy
ś
wietla si
ę
komunikat o b
łę
dzie " dEL Error ", a
dane chronione w pami
ę
ci pozostan
ą
bez zmian.
Korygowanie danych
Aby wej
ść
w tryb EDIT, naci
ś
nij [ 2nd ] [ EDIT ].
W trybie EDIT mo
ż
esz
obejrze
ć
, skogygowa
ć
lub wykasowa
ć
dane.
(A) W trybie 1–VAR sposób przegl
ą
dania danych zale
ż
y od tego czy
chcesz obejrze
ć
indywidualne dane czy te
ż
nie.
# Po ka
ż
dym nacisni
ę
ciu klawisza [ DATA ] w ci
ą
gu 1 sekundy
wy
ś
wietla si
ę
nazwa pierwszej warto
ś
ci a potem wprowadzona
liczba.
[ DATA ]
DEG
dAtA 1
STAT
EDIT
1 second
DEG
15.
STAT
EDIT
# Po ka
ż
dym nacisni
ę
ciu klawisza [ = ] wprowadzona liczba
bezpo
ś
rednio wy
ś
wietla sie na ekranie.
[ = ]
DEG
15.
STAT
EDIT
-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po33-
(B) W
trybie
REG po ka
ż
dym nacisni
ę
ciu klawisza [ DATA ] na ekranie
równocze
ś
nie wy
ś
wietlaj
ą
nazwa warto
ś
ci i wprowadzona liczba x.
Do prze
łą
czenia pomi
ę
dzy danymi x a y s
ł
u
ż
y klawisz [ ].
[ DATA ]
DEG
DATA 1 = 15 , 45
STAT
15
EDIT
[ ]
DEG
DATA 1 = 15 , 45
STAT
451
EDIT
Je
ś
li chcesz skorygowa
ć
dane, po prostu znajd
ź
żą
dan
ą
warto
ść
i
zamie
ń
j
ą
now
ą
warto
ś
ci
ą
.
Komunikat FULL
Komunikat „FULL” wy
ś
wietla si
ę
kiedy zaistniej
ą
poni
ż
sze warunki i
wprowadzenie danych b
ę
dzie niemo
ż
liwe.
Naci
ś
nij dowolny klawisz
aby zlikwidowa
ć
b
łą
d.
Poprzednio wprowadzone dane pozostan
ą
bez
zmian dopóki nie wyjdziesz z trybu STAT.
1) Je
ś
li liczba danych wprowadzonych naci
ś
ni
ę
ciem klawisza
[ DATA ] przewy
ż
sza 50
2) Liczba
powtórze
ń
przewy
ż
sza 255
3) n
>
12750 (n = 12750 pojawia si
ę
, je
ś
li klawisz [ DATA ] naci
ś
ni
ę
to
wi
ę
cej ni
ż
50 razy, a liczba powtórze
ń
ka
ż
dej warto
ś
ci stanowi
255, i.e. 12750 = 50 x 255 )
Operacje na liczbach zespolonych
Operacje na liczbach zespolonych dokonywane s
ą
w trybie CPLX
( [ MODE ] 3 ( CPLX ) ).
Liczby zespolone mo
ż
na dodawa
ć
, odejmowa
ć
, mno
ż
y
ć
i dzieli
ć
.
Wyniki operacji na liczbach zespolonych wy
ś
wietlane s
ą
w
nast
ę
puj
ą
cy sposób:
Re Warto
ść
rzeczywista
Im Warto
ść
urojona
ab Warto
ść
absolutna
ar
Warto
ść
argumentu
¾
( 7 – 9 i ) + ( 15 + 12 i ) = 22 + 3 i , ab = 22.2036033112,
ar = 7.76516601843
CPLX
DEG
[ MODE ] 3
0
.
CPLX
DEG
R e
I m
a b
a r
7 [ – ] 9 [ i ] [ + ] 15 [ + ] 12 [ i ] [ = ]
2 2
.
CPLX
DEG
R e
I m
a b
a r
[
]
3
.
i

-SR260B_SR-281N_Polish_v090331.doc SIZE: 140x75mm SCALE 1:1
2009/4/1
-Po34-
CPLX
DEG
R e
I m
a b
a r
[
]
2 2
.
2 0 3 6 0 3 3 1 1 2
CPLX
DEG
R e
I m
a b
a r
[
]
7
.
7 6 5 1 6 6 0 1 8 4 3

WEEE MARK
En
If you want to dispose this product, do not mix with general household
waste. There is a separate collection systems for used electronics products
in accordance with legislation under the WEEE Directive (Directive
2002/96/EC) and is effective only within European Union.
Ge
Wenn Sie dieses Produkt entsorgen wollen, dann tun Sie dies bitte nicht
zusammen mit dem Haushaltsmüll. Es gibt im Rahmen der WEEE-
Direktive innerhalb der Europäischen Union (Direktive 2002/96/EC)
gesetzliche Bestimmungen für separate Sammelsysteme für gebrauchte
elektronische Geräte und Produkte.
Sp
Si desea deshacerse de este producto, no lo mezcle con residuos
domésticos de carácter general. Existe un sistema de recogida selectiva
de aparatos electrónicos usados, según establece la legislación prevista
por la Directiva 2002/96/CE sobre residuos de aparatos eléctricos y
electrónicos (RAEE), vigente únicamente en la Unión Europea.
It
Se desiderate gettare via questo prodotto, non mescolatelo ai rifiuti
generici di casa. Esiste un sistema di raccolta separato per i prodotti
elettronici usati in conformità alla legislazione RAEE (Direttiva
2002/96/CE), valida solo all’interno dell’Unione Europea.
Du
Deponeer dit product niet bij het gewone huishoudelijk afval wanneer u het
wilt verwijderen. Erbestaat ingevolge de WEEE-richtlijn (Richtlijn
2002/ 96/EG) een speciaal wettelijk voorgeschreven verzamelsysteem
voor gebruikte elektronische producten, welk alleen geldt binnen de
Europese Unie.
JM74932-00F
Da
Hvis du vil skille dig af med dette produkt, må du ikke smide det ud sammen
med dit almindelige husholdningsaffald. Der findes et separat indsamlingssys-
tem for udtjente elektroniske produkter i overensstemmelse med
lovgivningen under WEEE-direktivet (direktiv 2002/96/EC), som kun er
gældende i den Europæiske Union.
Por
Se quiser deitar fora este produto, não o misture com o lixo comum. De acordo
com a legislação que decorre da Directiva REEE – Resíduos de Equipamen-
tos Eléctricos e Electrónicos (2002/96/CE), existe um sistema de recolha
separado para os equipamentos electrónicos fora de uso, em vigor apenas
na União Europeia.
Pol
Fr
Si vous souhaitez vous débarrasser de cet appareil, ne le mettez pas à la
poubelle avec vos ordures ménagères. Il existe un système de
récupération distinct pour les vieux appareils électroniques conformé-
ment à la législation WEEE sur le recyclage des déchets des
équipements électriques et électroniques (Directive 2002/96/EC) qui est
uniquement valable dans les pays de l’Union européenne.
Les appareils et les machines électriques et électroniques contiennent
souvent des matières dangereuses pour l’homme et l’environnement si vous
les utilisez et vous vous en débarrassez de façon inappropriée.
C‑Type(Scientific)
135x75mm


