Citizen SR-281N: Inhaltsverzeichnis
Inhaltsverzeichnis: Citizen SR-281N

SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G1-
Allgemeine Erläuterungen ................................................................ 2
Ein- und Ausschalten ....................................................................... 2
Batteriewechsel ............................................................................... 2
Auto-Abschaltfunktion ...................................................................... 2
Rückstellvorgang ............................................................................. 2
Regeln des Kontrastes .................................................................... 3
Bildschirmanzeige............................................................................ 3
Vor dem Start einer Berechnung...................................................... 3
Die Verwendung der " MODUS " Tasten .......................................... 3
Die Verwendung der Taste " 2nd " ................................................... 4
Korrekturen ...................................................................................... 4
Die Rückgängig-Funktion................................................................. 4
Die Wiederholen-Funktion ............................................................... 5
Speicherkalkulationen...................................................................... 5
Reihenfolge der Operationen........................................................... 6
Genauigkeit und Kapazität............................................................... 7
Fehlerbedingungen.......................................................................... 9
Basisberechnungen .......................................................................... 9
Arithmetische Berechnungen........................................................... 9
Klammerrechnungen ..................................................................... 10
Prozentrechnung ........................................................................... 10
Anzeigeformate.............................................................................. 11
Wissenschaftliche Berechnungen ................................................. 12
Logarithmus und Antilogarithmus................................................... 12
Bruchrechnen ................................................................................ 13
Konvertierung von Winkeleinheiten ............................................... 14
Umrechnung Sexagesimal
↔
Dezimal .......................................... 14
Winkel- / Umkehrwinkelfunktionen................................................. 15
Hyperbel / Umkehrhyperbelfunktionen........................................... 15
Koordinatentransformation............................................................. 16
Wahrscheinlichkeitsrechnung ........................................................ 16
Andere Funktionen ( 1/x,
,
3
,
X
, x
2
, x
3
, x
y
, INT, FRAC ).... 17
Einheitenkonvertierung .................................................................. 18
Physikkonstanten........................................................................... 18
Basis–n Berechnungen .................................................................. 24
Basiskonversionen......................................................................... 25
Block-Funktion ............................................................................... 25
Grundlegende arithmetische Operationen für Basen..................... 27
Negative Werte .............................................................................. 27
Logische Operation........................................................................ 27
Statistische Berechnungen ............................................................ 27
Dateneingabe ................................................................................ 28
Ergebnisanzeige ............................................................................ 28
Daten löschen................................................................................ 31
Daten bearbeiten ........................................................................... 32
Der Hinweis FULL.......................................................................... 32
Komplexe Berechnungen ............................................................... 33
Inhaltsverzeichnis

SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G2-
Allgemeine
Erläuterungen
Ein- und Ausschalten
Um den Rechner einzuschalten, dr
ü
cken Sie [ ON/C ]; um den
Rechner auszuschalten, dr
ü
cken Sie [ 2nd ] [ OFF ].
Batteriewechsel
Der Rechner wird mit zwei G13(LR44) Alkali-Batterien versorgt. Falls
der Bildschirm schwächer wird, wechseln Sie die Batterien aus. Seien
Sie vorsichtig, damit Sie sich beim Wechseln der Batterien nicht
verletzen.
1. Lösen Sie die Schrauben an der Rückseite des Rechners.
2. Führen Sie einen flachen Schraubenzieher in den Schlitz zwischen
der oberen und unteren Kante, drehen Sie ihn, um die Abdeckung
zu vorsichtig zu öffnen.
3. Entnehmen Sie beide Batterien und entsorgen Sie sie auf korrekte
Weise. Achten Sie darauf, dass Kinder nicht mit den Batterien
spielen.
4. Wischen Sie mit einem trockenen Tuch über die neuen Batterien,
um die Kontaktfähigkeit zu erhöhen.
5. Legen Sie die zwei neuen Batterien mit der flachen Seite aufrecht
(Plus Pole) ein.
6. Bringen Sie beide Kanten in Übereinstimmung und lassen Sie sie
zusammenschnappen.
7. Ziehen Sie die Schrauben an.
Auto-Abschaltfunktion
Der Rechner schaltet sich nach etwa 6~9 Minuten Inaktivität
automatisch aus. Ein Drücken der [ ON/C ] Taste reaktiviert den
Rechner; Bildschirm, Speicher und Einstellungen bleiben erhalten.
Rückstellvorgang
Falls Sie bei eingeschaltetem Rechner unerwartete Ergebnisse
bekommen, dr
ü
cken Sie der Reihe nach [ MODE ] [ 4 ] ( RESET ).
Eine Bildschirmnachricht fordert zur Bestätigung der Rückstellung des
Rechners und der Löschung aller Speicherinhalte auf.
RESET : N Y
Bewegen Sie den Cursor zu " Y " durch [ ], dr
ü
cken Sie [ = ], um
alle Variablen, aktuelle Vorgänge, statistische Daten, Antworten, alle
vorherigen Eingaben und den Speicher zu löschen. Um den
Rückstellvorgang abzubrechen, und nichts zu löschen, wählen Sie "N".
Ist der Rechner gesperrt und weitere Tastatureingaben somit
unmöglich, drücken Sie mit einem spitzen Gegenstand in die
Rückstellungsöffnung, um diesen Zustand aufzuheben. Alle
Einstellungen werden auf die Standardeinstellungen zurückgestellt.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G3-
Regeln des Kontrastes
Durch Drücken von [ – ] oder [ + ] nach Bedienen der [ MODE ] Taste
wird der Kontrast des Bildschirms, d.h. die Helligkeit, erhöht oder
verringert.
Bildschirmanzeige
Der Bildschirm besteht aus zwei Zeilen und Indikatoren. Die obere
Zeile ist eine Punktanzeige mit bis zu 128 Zeichen. Die untere Zeile
kann bis zu 12 Stellen und auch 2-stelige positive oder negative
Exponenten anzeigen.
Mit [ = ] eingegebene Formeln und Berechnungen erscheinen in der
oberen Zeile, das Ergebnis wird in der unteren Zeile angezeigt.
Folgende Indikatoren erscheinen auf dem Bildschirm, um den
aktuellen Status des Rechners anzugeben.
Indikator Bedeutung
M Aktueller
Speicher
–
Ergebnis ist negativ
E Fehler
STO
Der Modus ‚Variablen Speichern’ ist aktiv
RCL
Der Modus ‚Variablen Abrufen’ ist aktiv
2nd
2. Set der Funktionstasten ist aktiv
HYP
Hyperbel-trigonometrische Funktion wird berechnet
ENG Techniksymbolnotation
CPLX
Der Modus Komplexe Zahlen ist aktiv
CONST
Zeigt Physikkonstanten an
DEGRAD
Winkelmodus: Grade, Gradianten, oder Radianten
BIN Binäre
Basis
OCT Oktale
Basis
HEX Hexadezimale
Basis
( )
Offene Klammer
TAB
Anzahl der angezeigten Dezimalstellen ist festgelegt
STAT Statistikmodus
ist
aktiv
REG Regressionsmodus
ist
aktiv
EDIT
Statistische Daten werden ausgewertet
CPK
CPK: Verarbeitungsfähigkeit
CP:
Präzisionsfähigkeit
USL Oberes
Spezifikationslimit
setzen
LSL
Unteres Spezifikationslimit setzen
i Fiktiver
Teil
Rückgängig-Funktion
aktiviert
Vor dem Start einer Berechnung
Die Verwendung der " MODUS " Tasten

SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G4-
Dr
ü
cken Sie [ MODE ], um die Modusmenüs anzuzeigen, um ein
Betriebsmodus ( " 1 MAIN ", " 2 STAT ", " 3 CPLX ", " 4 RESET " )
oder Techniksymbolnotation ( " 5 ENG " ) zu wählen.
1 MAIN: Nutzen Sie diesen Modus für grundlegende
Berechnungen, inklusive wissenschaftlicher
Berechnungen und Basis–n Berechnungen.
2 STAT: Nutzen Sie diesen Modus, um einzelvariable und
paarvariable statistische Berechnungen und
Regressionsberechnungen auszuführen.
3 CPLX: Nutzen Sie diesen Modus, um komplexe
Zahlenberechnungen auszuführen.
4 RESET: Nutzen Sie diesen Modus, um die Rücksetzfunktion
auszuführen.
5 ENG:
Nutzen Sie diesen Modus, um Technikberechnungen mit
Hilfe von Techniksymbolen zuzulassen.
Hier ist " 2 STAT " als Beispiel:
Methode 1: Drücken Sie [ MODE] und scrollen Sie mit [
] oder
[ 2nd ] [
] durch die Menüs, bis " 2 STAT "
unterstrichen ist, aktivieren Sie den gewünschten Modus
mit [ = ].
Methode 2: Drücken Sie [ MODE] und geben Sie die Zahl des
Modus, [ 2 ] direkt ein, um den gewünschten Modus
sofort zu aktivieren.
Die Verwendung der Taste " 2nd "
Wenn Sie [ 2nd ] drücken, zeigt der " 2nd " Indikator auf dem
Bildschirm an, dass die zweite Funktion der nächsten gedrückten
Taste aktiv ist. Ein irrtümliches Drücken der Taste [ 2nd ], kann durch
erneutes Drücken der [ 2nd ] Taste rückgängig gemacht werden.
Korrekturen
Falls bei der Eingabe einer Zahl ein Fehler unterläuft (jedoch noch
keine arithmetische Operationstaste gedrückt wurde), dr
ü
cken Sie
einfach [ CE ], um die letzte Eingabe zu löschen, wiederholen Sie nun
die Eingabe, oder löschen Sie weitere individuelle Stellen mit der
Backspace-Taste [
], oder löschen Sie alle Eingaben mit [ ON/C ].
Wenn nach der Korrektur die Eingabe der Formel komplett ist,
erhalten Sie die Antwort durch Drücken von [ = ]. Sie können auch
[ ON/C ] drücken, um das Ergebnis komplett zu löschen (den Speicher
ausgenommen). Das Drücken einer falschen arithmetischen
Betriebstaste kann durch Bedienen der richtigen Taste korrigiert
werden.
Die Rückgängig-Funktion
Mit dieser Funktion können einige Fehler rückgängig gemacht werden.
Wurde ein Zeichen mit [ ], eine Eingabe mit [ CE ], oder [ ON/C ]
gelöscht, zeigt der "
" Indikator an, dass dieser Vorgang mit
Drücken von [ 2nd ] [
] rückgängig gemacht werden kann.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G5-
Die Wiederholen-Funktion
Diese Funktion speichert gerade ausgeführte Operationen. Nach dem
Ende der Ausführungen kann die Operation durch Drücken von [ ]
oder [ 2nd ] [
] angezeigt werden. Drücken Sie [ ] wird die
Operation vom Anfang angezeigt und der Cursor unter das erste
Zeichen platziert. Drücken Sie [ 2nd ] [
] wird das Ende der
Operation angezeigt und der Cursor befindet sich in der Leerstelle
nach dem letzten Zeichen. Der Cursor kann mit [ ] oder [ 2nd ]
[
] weiter bewegt werden. Werte oder Befehle können für folgende
Ausführungen verändert oder eingegeben werden.
Speicherkalkulationen
Speichervariablen
Der Rechner hat neun Speichervariablen für sich wiederholende
Berechnungen -- A, B, C, D, E, F, M, X, Y. Sie können eine reale Zahl
in jedem dieser neun Speichervariablen speichern.
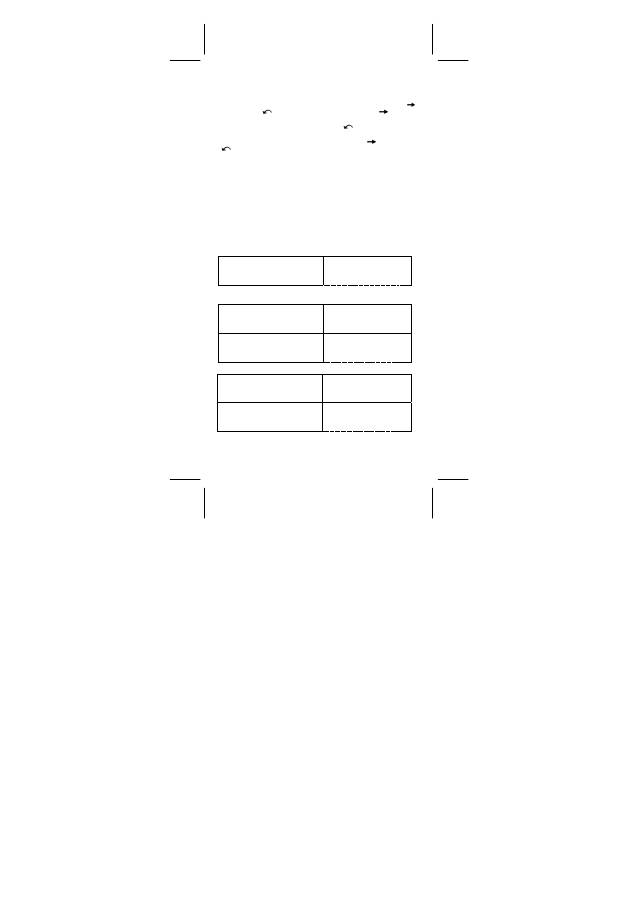
• [ STO ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] ermöglicht das Speichern von
Werten in Variablen.
• [ RCL ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] ruft den Wert der Variablen auf.
• [ 0 ] [ STO ] + [ A ] ~ [ F ], [ M ], [ X ] ~ [ Y ] löscht den Inhalt einer
spezifischen Speichervariablen.
¾
(1) Um den Wert 30 in der Variablen A zu speichern.
DEG
3 0
Æ
A
30 [ STO ] [ A ]
3 0
.
¾
(2) Die mehrfache 5 zur Variablen A, dann das Ergebnis in die
Variable B speichern
DEG
5
¼
A =
5 [ x ] [ RCL ] [ A ] [ = ]
1 5 0
.
DEG
1 5 0
Æ
B
[ STO ] [ B ]
1 5 0 .
¾
(3) Löscht den Wert der Variablen B
DEG
0
Æ
B
0 [ STO ] [ B ]
0
.
DEG
B =
[ RCL ] [ B ] [ = ]
0
.
Laufender Speicher
Beachten Sie bei der Nutzung des laufenden Speichers folgende
Regeln.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G6-
•
Drücken Sie [ M+ ], um dem laufenden Speicher ein Ergebnis
hinzuzufügen. Der "M" Indikator erscheint, wenn eine Nummer im
Speicher gespeichert ist. Um den Inhalt des laufenden Speichers
aufzurufen, drücken Sie [ MR ].
• Rückruf vom laufenden Speicher durch Drücken der [ MR ] Taste
ändert nicht seinen Inhalt.
• Im Statistikmodus ist bei laufendem Speicher nicht verfügbar.
• Die Speichervariable M und laufender Speicher nutzen den gleichen
Speicherbereich.
• Um den Inhalt des Speichers durch die angezeigte Zahl zu ersetzen,
dr
ü
cken Sie die [ X M ] Taste.
• Um den Inhalt des laufenden Speichers zu löschen, drücken Sie [ 0 ]
[ X M ], [ ON/C ] [ X M ] or [ 0 ] [ STO ] [ M ] in dieser Reihenfolge.
¾
[ ( 3 x 5 ) + ( 56 7 ) + ( 74 – 8 x 7 ) ] = 41
DEG
0 [ X M ]
0
.
DEG
7 4 – 8
¼
7 M +
3 [ x ] 5 [ M+ ] 56 [ ] 7 [ M+ ] 74
[ – ] 8 [ x ] 7 [ M+ ]
M
1 8
.
DEG
M
[ MR ]
M
4 1
.
DEG
0 [ X M ]
0
.
(Hinweis): Neben Drücken der [ STO ] oder [ X M ] Taste, zum
Speichern eines Wertes, kann man der Speichervariablen M
mit [ M+ ] Werte zuweisen. Bei der Benutzung von [ STO ]
[ M ] oder [ X M ] wird der alte Speicherinhalt der Variablen
M gelöscht und durch den neuen Wert ersetzt. Bei
Benutzen von [ M+ ] werden dem Speicher Werte
hinzugefügt.
Reihenfolge der Operationen
Jede Berechnung wird in der folgenden Reihenfolge ausgeführt:
1) Brüche
2) Ausdrücke innerhalb von Klammern.
3) Koordinatentransformation ( P R , R P )
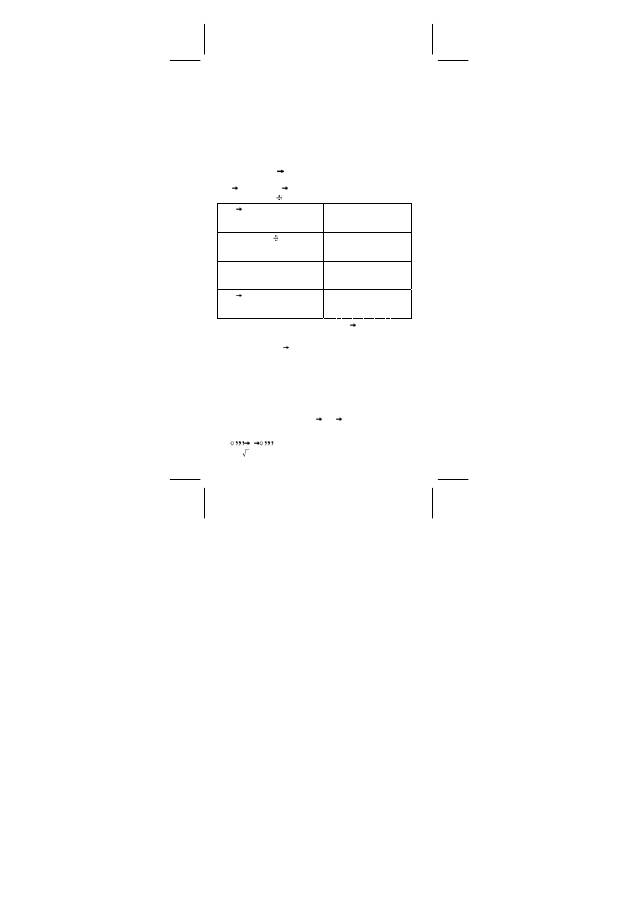
4) Typ A Funktionen, bei denen Werte eingegeben müssen, bevor
die Funktionstaste gedrückt wird, z.B. x
2
,1/x,
π
, x!, %, RND, ENG,
,
, x ', y ' .
5) x
y
,
X
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G7-
6) Typ B Funktionen, bei denen die Funktionstaste vor der Eingabe
gedrückt werden muss, z.B. sin, cos, tan, sin
–1
, cos
–1
, tan
–1
,
sinh, cosh, tanh, sinh
–1
, cosh
–1
, tanh
–1
, log, ln, FRAC, INT,
√
,
3
, 10
X
, e
X
, NOT, EXP, DATA im STAT Modus.
7) +/–,
NEG
8) nPr, nCr
9) x
,
10) +, –
11) AND, NAND –-- nur im Basis–n Modus
12) OR, XOR, XNOR --- nur im Basis–n Modus
Genauigkeit und Kapazität
Ausgabe: bis zu 12 Ziffern.
Berechnung: bis zu 14 Ziffern
Im Allgemeinen wird jede vernünftige Berechnung bis zu 12-Ziffern
Mantisse, oder 12-Ziffern Mantisse plus 2-Ziffern Exponent bis zu
10
±99
angezeigt.
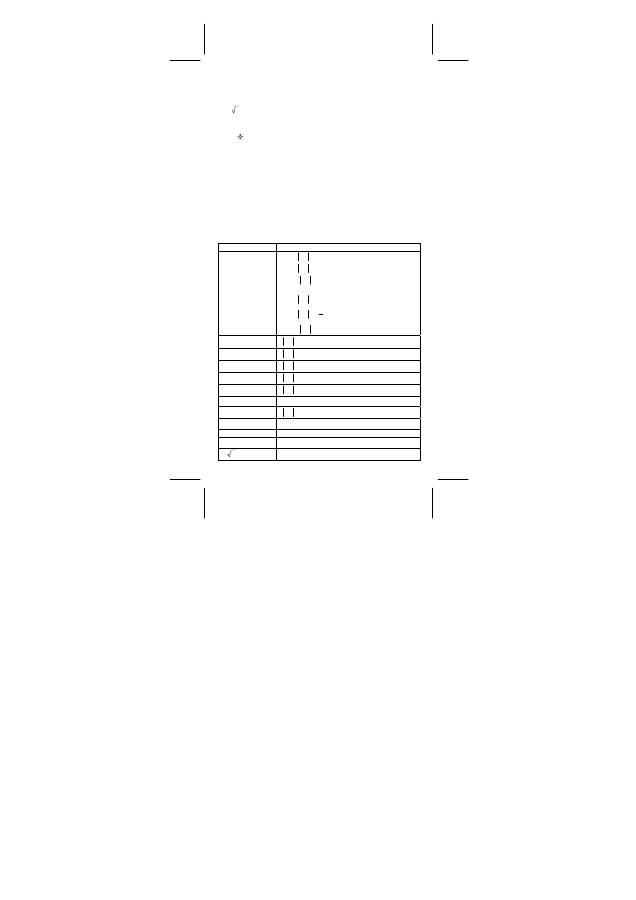
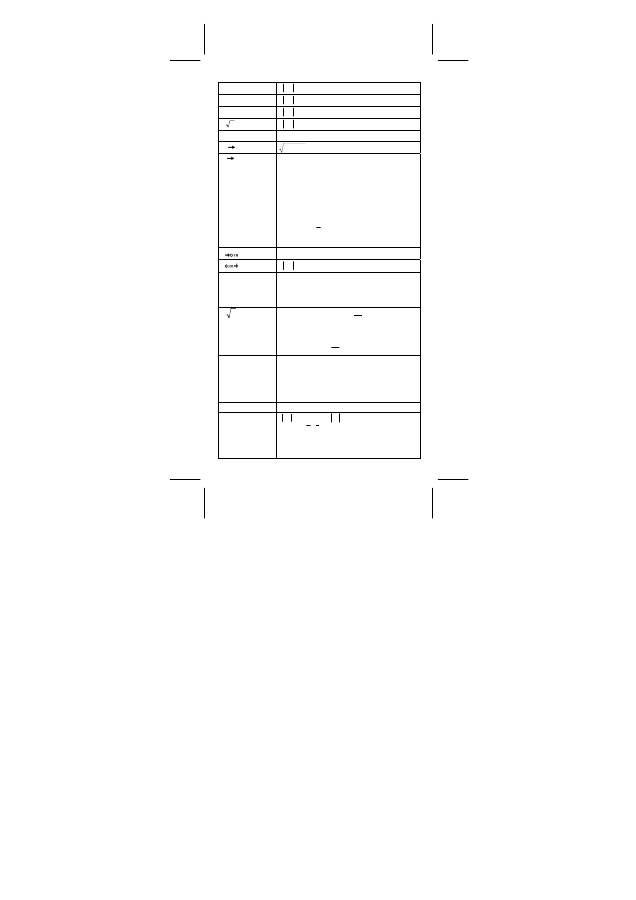
Die eingegebenen Zahlen müssen innerhalb des Bereichs der
gegebenen Funktion wie folgt sein:
Funktion Eingabebereich
sin x
cos x
tan x
Deg:
x
<
4.5 x 10
10
deg
Rad:
x
<
2.5 x 10
8
π
rad
Grad:
x
<
5 x 10
10
grad
aber, für tan x
Deg:
x
≠
90 (2n+1)
Rad:
x
≠
2
π
(2n+1)
Grad:
x
≠
100 (2n+1), (n ist ein Integer)
sin
–1
x, cos
–1
x
x
≦
1
tan
–1
x
x
<
1 x 10
100
sinh x, cosh x
x
≦
230.2585092
tanh x
x
<
1 x 10
100
sinh
–1
x
x
<
5 x 10
99
cosh
–1
x
1
≦
x
<
5 x 10
99
tanh
–1
x
x
<
1
log x, ln x
1 x 10
–99
≦
x
<
1 x 10
100
10
x
–1 x 10
100
<
x
<
100
e
x
–1 x 10
100
<
x
≦
230.2585092
x
0
≦
x
<
1 x 10
100
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G8-
x
2
x
<
1 x 10
50
x
3
x
<
2.15443469003 x 10
33
1/x
x
<
1 x 10
100
, x
≠
0
3
x
x
<
1 x 10
100
x !
0
≦
x
≦
69, x ist ein Integer.
R P
2
2
y
+
x
<
1 x 10
100
P R
0
≦
r
<
1 x 10
100
Deg
:
│
θ
│
<
4.5 x 10
10
deg
Rad
:
│
θ
│
<
2.5 x 10
8
π
rad
Grad
:
│
θ
│
<
5 x 10
10
grad
aber, für tan x
Deg
:
│
θ
│
≠
90 (2n+1)
Rad
:
│
θ
│
≠
2
π
(2n+1)
Grad
:
│
θ
│
≠
100 (2n+1), (n ist ein Integer)
│
D
│
, M, S
<
1 x 10
100
, 0
≦
M, S
x
<
1 x 10
100
x
y
x
>
0 : –1 x 10
100
<
y log x
<
100
x = 0 : y
>
0
x
<
0 : y = n, 1/(2n+1), n ist ein Integer.
aber –1 x 10
100
<
y log
│
x
│
<
100
x
y
y
>
0 : x
≠
0, –1 x 10
100
<
x
1
log y
<
100
y = 0 : x
>
0
y
<
0 : x=2n+1, l/n, n ist ein Integer.(n
≠
0)
aber –1 x 10
100
<
x
1
log
│
y
│
<
100
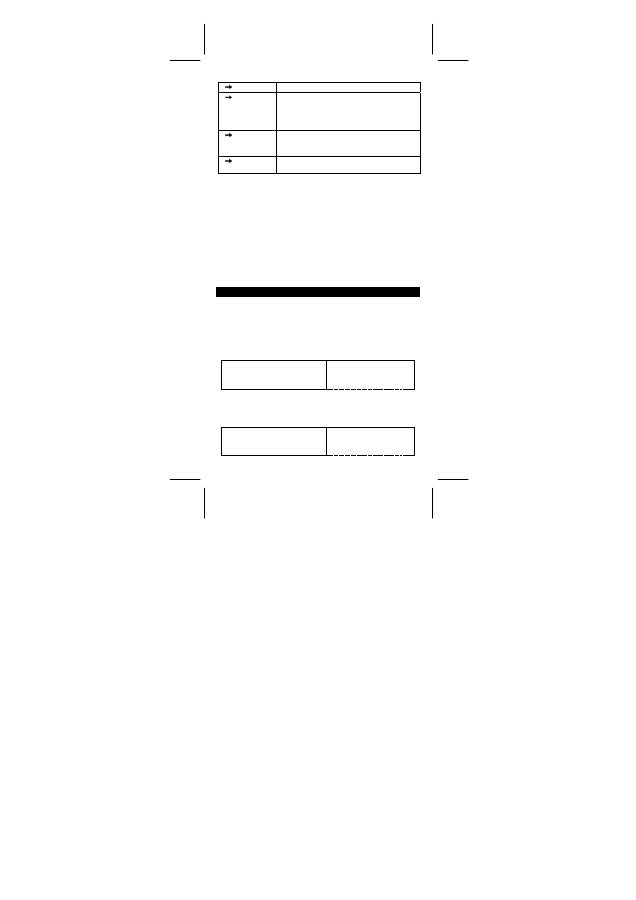
a b/c
Eingabe
:
Gesamtheit des Integers, Zählers
und Nenners kann 12 Stellen (inklusive
Trennstrich) nicht übersteigen
Ergebnis
:
Das Ergebnis wird als Bruch
dargestellt, wenn Integer, Zähler und Nenner
geringer als 1 x 10
12
betragen
nPr, nCr
0
≦
r
≦
n, n
≦
10
100
, n,r sind Integer.
STAT
x
<
1 x 10
50
,
y
<
1 x 10
50
σ
x,
σ
y,
x
, y , a, b, r : n
≠
0 ;
Sx, Sy
:
n
≠
0, 1 ; x
n
= 50 ; y
n
= 50 ;
Anzahl der Wiederholungen
≤
255, n ist ein
Integer.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G9-
DEC
– 2147483648
≦
x
≦
2147483647
BIN
0
≦
x
≦
01111111111111111111111111111111
(für Null, positiv)
10000000000000000000000000000000
≦
x
≦
11111111111111111111111111111111
(für negativ)
OCT
0
≦
x
≦
17777777777 (für Null oder positiv)
20000000000
≦
x
≦
37777777777
(für negativ)
HEX
0
≦
x
≦
7FFFFFFF (für Null oder positiv)
80000000
≦
x
≦
FFFFFFFF (für negativ)
Fehlerbedingungen
Liegt eine der folgenden Bedingungen vor, erscheint die
Fehlermeldung “
E
” auf dem Bildschirm und weitere Berechnungen
sind nicht möglich.
1) Sie haben versucht, durch 0 zu dividieren
2) Wenn der mögliche Eingabebereich der Funktionsberechnung
den angegebenen Bereich übersteigt
3) Wenn das Ergebnis der Funktionsberechnung den angegebenen
Bereich übersteigt
4) Wenn die [ ( ] Taste in mehr als 13 Ebenen in einem einzigen
Ausdruck benutzt wird
5) Wenn
USL
Wert
<
LSL Wert
Um die obengenannten Fehler freizugeben, drücken Sie [ ON/C ].
Basisberechnungen
Nutzen Sie den MAIN ( [ MODE ] 1 ( MAIN ) ) Modus für
Basisberechnungen.
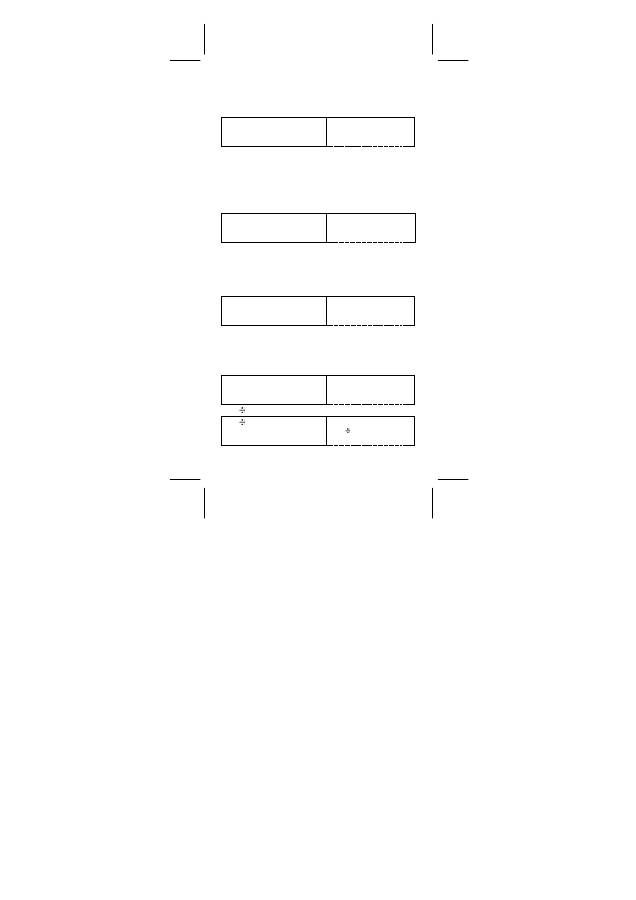
Arithmetische Berechnungen
Arithmetische Operationen werden durch Drücken der Tasten in der
Reihenfolge des folgenden Ausdrucks ausgeführt.
¾
7 + 5 x 4 = 27
DEG
7 + 5
¼
4 =
7 [ + ] 5 [ x ] 4 [ = ]
2 7
.
Um negative Werte anzugeben, dr
ü
cken Sie [ +/– ] nach der
Werteingabe; sie können eine Zahl in Mantisse oder Exponentenform
mit der [ EXP ] Taste eingeben.
¾
2.75 x 10
– 5
= 0.0000275
DEG
2
.
7 5 E – 0 5 =
2.75 [ EXP ] 5 [ +/– ] [ = ]
0
.
0 0 0 0 2
7 5
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G10-
Ergebnisse die 10
12
bzw. 10
–11
über- oder unterschreiten werden in
exponentieller Form dargestellt.
¾
12369 x 7532 x 74010 = 6895016425080
= 6.89501642508 x 10
12
DEG
1 2 3 6 9
¼
7 5 3 2
¼
7
12369 [ x ] 7532 [ x ] 74010
[=]
6
.
8 9 5 0 1 6 4 2 5 0 8
12
Klammerrechnungen
Operationen in einer Klammer werden immer zuerst ausgeführt.
SR-281N
kann bis zu 13 Ebenen aufeinanderfolgender Klammern in
einer einzigen Berechnung nutzen.
Geschlossene Klammern, die direkt vor Betätigen der [ ) ] Taste
gesetzt werden, kann man weglassen, unabhängig von der Anzahl.
¾
2 x { 7 + 6 x ( 5 + 4 ) } = 122
DEG
2
¼
( 7 + 6
¼
( 5 + 4 =
2 [ ( ] 7 [ + ] 6 [ ( ] 5 [ + ] 4 [ = ]
1 2 2
.
(Hinweis): Ein direkt vor einer offenen Klammer stehendes
Multiplikationszeichen "
x
" kann weggelassen werden.
Das korrekte Ergebnis kann nicht durch die Eingabe von [ ( ] 2 [ + ] 3
[ ) ] [ EXP ] 2 abgeleitet werden. Sie sollten, wie im folgenden Beispiel
gezeigt, [ x ] zwischen [ ) ] und [ EXP ] angeben.
¾
( 2 + 3 ) x 10
2
= 500
DEG
( 2 + 3 )
¼
1 E 0 2 =
[ ( ] 2 [ + ] 3 [ ) ] [ x ] [ EXP ] 2
[ = ]
5
0 0
.
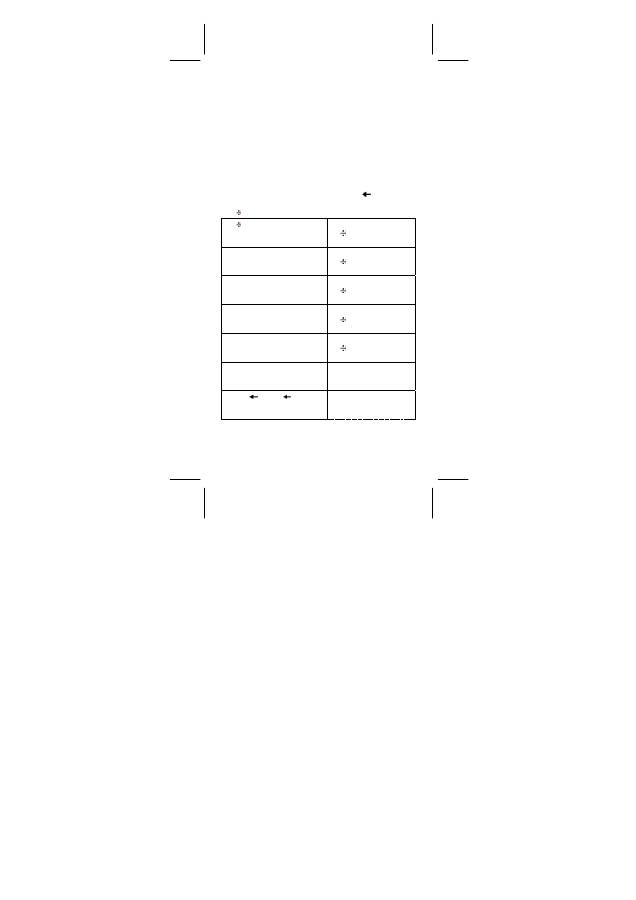
Prozentrechnung
[ 2nd ] [ % ] teilt die Zahl in der Anzeige durch 100. Sie können diese
Tastenfolge verwenden, um Prozentsätze, Zugaben, Rabatte und
Prozentualverhältnisse zu berechnen.
¾
120 x 30 % = 36
DEG
1 2 0
¼
3 0 % =
120 [ x ] 30 [ 2nd ] [ % ] [ = ]
3 6
.
¾
88 55 % = 160
DEG
8 8
5 5 % =
88 [ ] 55 [ 2nd ] [ % ] [ = ]
1 6 0
.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G11-
Anzeigeformate
Der Rechner arbeitet mit folgenden Anzeigeformaten zur Anzeige der
Werte.
Fix / Gleitkomma
Um eine Anzahl von Dezimalstellen festzulegen, drücken Sie [ 2nd ]
[ TAB ] und geben Sie einen Wert für die Anzahl der Stellen ( 0~9 ) an.
Werte werden bis an die angegebene Stelle abgerundet angezeigt.
Um zum Gleitkomma zurückzukehren, drücken Sie [ 2nd ] [ TAB ] [ • ].
Wissenschaftliche Notation
Drücken Sie [ F
↔
E ], um den Bildschirmmodus zwischen Gleitkomma
und wissenschaftlicher Notation zu schalten.
Technische Notation
Nach Drücken von [ ENG ] oder [ 2nd ] [
] wechselt die
Exponentenanzeige der Zahl zu einer Anzeige eines Vielfaches von 3.
¾
6 7 = 0.85714285714…
DEG
6
7 =
6 [ ] 7 [ = ]
0
.
8 5 7 1 4 2 8 5 7 1 4
DEG TAB
6
7 =
[ 2nd ] [ TAB ] 4
0 . 8 5 7 1
DEG TAB
6
7 =
[ 2nd ] [ TAB ] 2
0
.
8 6
DEG
6
7 =
[ 2nd ] [ TAB ] [ • ]
0
.
8 5 7 1 4 2 8 5 7 1 4
DEG
6
7 =
[ F
↔
E ]
8
.
5 7 1 4 2 8 5 7 1 4 3
–01
DEG
[ ENG ]
8 5 7
.
1 4 2 8 5 7 1 4 3
–03
DEG
[ 2nd ] [
] [ 2nd ] [
]
0
.
0 0 0 8 5 7 1 4 2 8 5
03
Technische Symbole
Nach jeder Aktivierung des ENG Modus wird das angezeigte Ergebnis
automatisch mit dem entsprechenden technischen Symbol versehen.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G12-
Y
yotta
= 10
24
,
Z
zetta
= 10
21
,
E
exa
= 10
18
,
P
peta
= 10
15
,
T
tera
= 10
12
,
G
giga
= 10
9
,
M
mega
= 10
6
,
K
kilo
= 10
3
,
m
milli
= 10
– 3
,
μ
micro
= 10
– 6
,
n
nano
= 10
– 9
,
p
pico
= 10
– 12
,
f
femto
= 10
– 15
,
a
atto
= 10
– 18
,
z
zepto
= 10
– 21
,
y
yocto
= 10
– 24
Führen Sie folgende Operation durch, um das technische Symbol zu
bestimmen.
[ MODE ] 5 ( ENG )
Um den Modus zu verlassen, drücken Sie erneut [ MODE ].
¾
6 7 = 0.85714285714…
ENG
DEG
[ MODE ] 5
0
.
ENG
DEG
6
7 =
m
6 [ ] 7 [ = ]
8
5
7
.
1 4 2 8 5 7 1
4 3
ENG
DEG
μ
[ ENG ]
8 5 7 1 4 2
.
8 5 7 1 4 3
ENG
DEG
K
[ 2nd ] [
] [ 2nd ] [
] [ 2nd ]
[
]
0
.
0 0 0 8 5 7 1 4 2 8 5
Wissenschaftliche
Berechnungen
Nutzen Sie den MAIN ( [ MODE ] 1 ( MAIN ) ) Modus für
wissenschaftliche Berechnungen.
Logarithmus und Antilogarithmus
Der Rechner kann normale und natürliche Logarithmen und
Antilogarithmen durch Verwendung von [ log ], [ ln ], [ 2nd ] [ 10
x
],
und [ 2nd ] [ e
x
] berechnen.
¾
ln 7 + log 100 = 3.94591014906
DEG
l n 7 + l o g 1 0 0 =
[ ln ] 7 [ + ] [ log ] 100 [ = ]
3
.
9 4 5 9 1 0 1 4 9 0 6
¾
10
2
+ e
–5
= 100.006737947
DEG
10
^ 2 + e ^ – 5 =
[ 2nd ] [ 10
X
] 2 [ + ] [ 2nd ] [ e
X
] 5
[ + / – ] [ = ]
1 0 0
.
0 0 6 7 3 7 9 4 7

SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G13-
Bruchrechnen
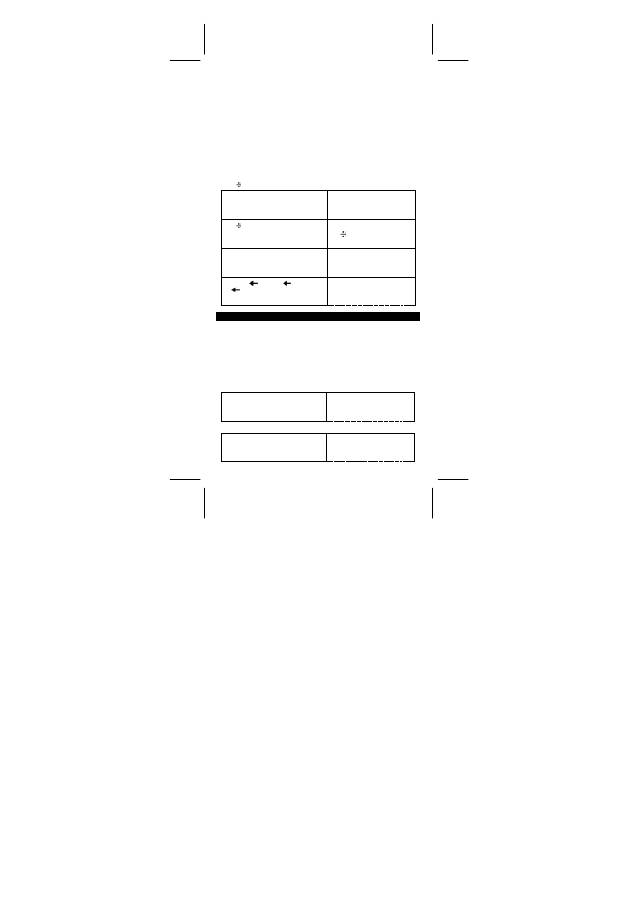
Bruchwerte werden in folgender Weise dargestellt:
5
」
12
Anzeige von
12
5
56
∪
5
」
12
Anzeige von 56
12
5
(Hinweis): Werte werden automatisch in Dezimalformat angezeigt,
wenn die Anzahl der Stellen des Bruchwertes ( Integer +
Zähler + Nenner + Trennzeichen ) 12 überschreitet.
Um eine gemischte Zahl einzugeben, geben Sie die ganze Zahl ein,
drücken Sie [ a b/c ], geben Sie den Zähler ein, drücken Sie [ a b/c ]
und geben Sie den Nenner ein; um einen unreinen Bruch einzugeben,
geben Sie den Zähler ein, drücken Sie [ a b/c ] und geben Sie Nenner
ein.
¾
21
8
22
7
5
14
3
2
7
=
+
DEG
7
2
3
+ 1 4
5
7
7 [ a b/c ] 2 [ a b/c ] 3 [ + ] 14 [ a b/c ]
5 [ a b/c ] 7 [ = ]
2 2
8
2 1
.
Wenn bei einer Bruchrechnung die Zahl gekürzt werden kann, wird sie
nach Drücken einer Befehlstaste ( [ + ], [ – ], [ x ] oder [ ] ) oder
[
] auf den niedrigsten Bruch gekürzt. Durch Drücken von [ 2nd ]
[ d/e ] wird der angezeigte Wert in einen unreinen Bruch konvertiert
und umgekehrt. Zur Konvertierung zwischen einem dezimalen und
einem Bruchergebnis drücken Sie [ a b/c ].
¾
2
9
5
.
4
2
1
4
4
2
4
=
=
=
DEG
4
2
4
=
4 [ a b/c ] 2 [ a b/c ] 4 [ = ]
4
1
2
.
DEG
4
2
4
=
[ a b/c ]
4
.
5
DEG
4
2
4
=
[ a b/c ] [ 2nd ] [ d/e ]
9
2
.
DEG
4
2
4
=
[ 2nd ] [ d/e ]
4
1
2
.
Berechnungen die sowohl Brüche als auch Dezimale enthalten,
werden in dezimalem Format berechnet.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G14-
¾
55
.
12
75
.
3
5
4
8
=
+
DEG
8
4
5
+ 3
.
7 5 =
8 [ a b/c ] 4 [ a b/c ] 5 [ + ] 3.75
[ = ]
1 2
.
5 5
Konvertierung von Winkeleinheiten
Der Rechner ermöglicht die Konvertierung zwischen den
Winkeleinheiten Grad(DEG), Radianten(RAD) und Gradianten
(GRAD).
Die Beziehung zwischen den drei Winkeleinheiten ist:
180 ° =
π
rad = 200 grad
1) Um die Voreinstellung zu ändern, dr
ü
cken Sie die [ 2nd ] [ DRG ]
Taste, bis die gewünschte Winkeleinheit im Bildschirm erscheint.
2) Drücken Sie nach der Eingabe eines Wertes [ 2nd ] [ DRG ], bis
die gewünschte Einheit angezeigt wird.
¾
90 deg. = 1.57079632679 rad. = 100 grad.
DEG
[ 2nd ] [ DRG ]
0
.
RAD
9 0
O
=
90 [ 2nd ] [ DRG ]
1 .
5 7 0 7 9 6 3 2 6 7 9
GRAD
1
.
5 7 0 7 9 6 3 2 6 7
[ 2nd ] [ DRG ]
1 0 0
.
Umrechnung Sexagesimal
↔
Dezimal
Der Rechner ermöglicht das Konvertieren sexagesimaler Werte (Grad,
Minuten und Sekunden) in dezimale Notierung durch Drücken von
[
]. Umgekehrt ist eine Konvertierung dezimaler Werte in
sexagesimale durch [ 2nd ] [
] möglich.
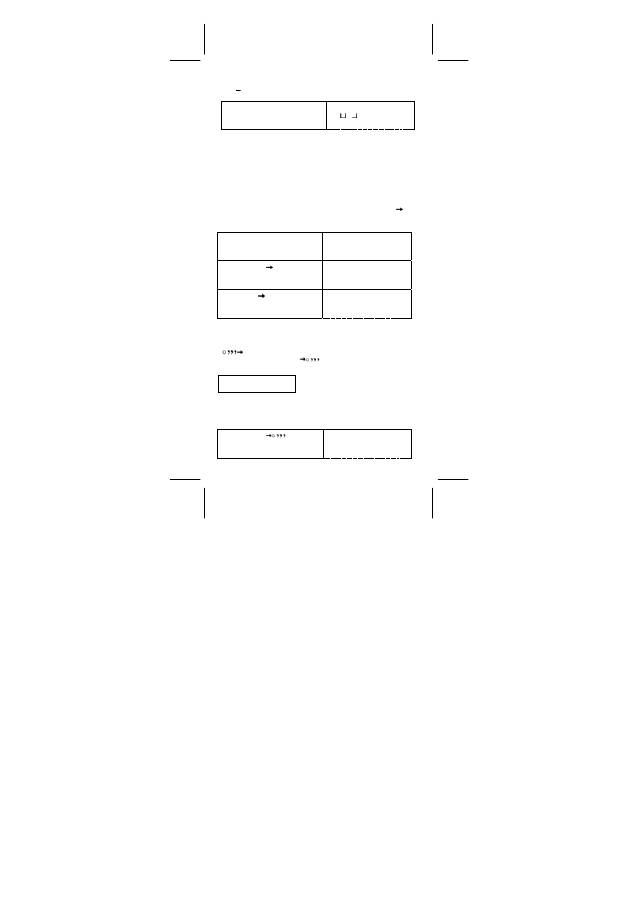
Sexagesimale Ziffernwerte werden wie folgt dargestellt:
125
45
׀
30
׀
׀
55
Steht für 125 Grad (D),
45 Minuten(M), 30.55 Sekonden(S)
(Hinweis): Übersteigt die Anzahl der D, M, S, inklusive
Trennmarkierung 10 Stellen, wird die Sexagesimalzahl nicht
komplett angezeigt.
¾
12.755 = 12
45
l
18
l l
DEG
12.755 [ 2nd ] [
]
1 2
4 5
l
1 8
l l
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G15-
¾
2
45
l
10.5
l l
= 2.75291666667
DEG
2 [
] 45 [
] 10.5 [
]
2
.
7 5 2 9 1 6 6 6 6 6 7
Winkel- / Umkehrwinkelfunktionen
SR-281N
ist in der Lage Standardwinkel- und
Umkehrwinkelfunktionen - sin, cos, tan, sin
–1
, cos
–1
und tan
–1
zu
berechnen.
(Hinweis): Wenn Sie diese Tasten verwenden, prüfen Sie, ob die
gewünschte Winkeleinheit eingestellt ist.
¾
sin 30 deg.= 0.5
DEG
s i n 3 0 =
[ sin ] 30 [ = ]
0
.
5
¾
3 cos (
π
3
2
rad) = – 1.5
RAD
3
¼
c o s ( 2
¼
π
3 =
3 [ cos ] [ ( ] 2 [ x ] [ 2nd ] [
π
] [ ]
3 [ = ]
– 1
.
5
¾
3 sin
–1
0.5 = 90 deg
DEG
3
¼
s i n
–1
0
.
5 =
3 [ 2nd ] [ sin
–1
] 0.5 [ = ]
9 0
.
Hyperbel / Umkehrhyperbelfunktionen
SR-281N
verwendet [ 2nd ] [ HYP ], um Hyperbelfunktionen und
Umkehrhyperbelfunktionen - sinh, cosh, tanh, sinh
–1
, cosh
–1
und
tanh
–1
zu berechnen.
(Hinweis): Wenn Sie diese Tasten verwenden, prüfen Sie, ob der
Rechner auf die gewünschte Winkeleinheit eingestellt ist.
¾
cosh 1.5 + 2 = 4.35240961524
DEG
c o s h 1
.
5 + 2 =
[ 2nd ] [ HYP ] [ cos ] 1.5 [ + ] 2 [ = ]
4
.
3 5 2 4 0 9 6 1 5 2 4
¾
sinh
–1
7 = 2.64412076106
DEG
s i n h 1
–1
7 =
[ 2nd ] [ HYP ] [ 2nd ] [ sin
–1
] 7 [ = ]
2
.
6 4 4 1 2 0 7 6 1 0 6
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G16-
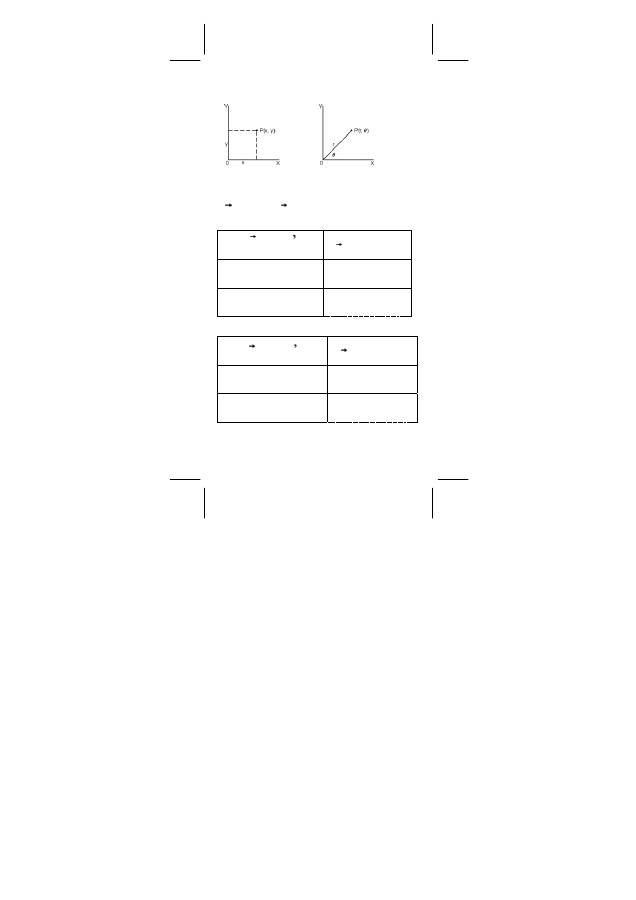
Koordinatentransformation
Rechteckige Koordinaten Polare Koordinaten
x + y i = r (cos
θ
+ i sin
θ
)
(Hinweis): Achten Sie bei der Benutzung dieser Taste darauf, dass die
gewünschte Winkeleinheit eingestellt ist.
Der Rechner konvertiert rechtwinklige und polare Koordinaten, [ 2nd ]
[ P R ] und [ 2nd ] [ R P ].
¾
Wenn x = 5, y = 30, was sind r,
θ
? Ans : r = 30.4138126515,
θ
= 80.537677792
o
DEG
( )
R
P ( 5
,
[ 2nd ]
[ R P ] 5 [ 2nd ] [ ] 30
3 0
DEG
r
[ = ]
3 0
.
4 1 3 8 1 2 6 5 1 5
DEG
θ
[ 2nd ] [ X
↔
Y ]
8 0
.
5 3 7 6 7 7 7 9 2
¾
Wenn r = 25,
θ
= 56
o
was sind x , y ? Ans : x = 13.9798225868,
y = 20.7259393139
DEG
( )
P
R ( 2 5
,
[ 2nd ] [ P R ] 25 [ 2nd ] [ ] 56
5 6
DEG
X
[ = ]
1 3
.
9 7 9 8 2 2 5 8 6 8
DEG
Y
[ 2nd ] [ X
↔
Y ]
2 0
.
7 2 5 9 3 9 3 1 3 9
Wahrscheinlichkeitsrechnung
Der Rechner führt folgende Wahrscheinlichkeitsrechnungen aus:
[ nPr ] berechnet die Anzahl der Permutationen von n-Elementen,
wobei jeweils die Anzahl r verwendet wird.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G17-
[ nCr ] berechnet die Anzahl der Kombinationen von n-Elementen,
wobei jeweils die Anzahl r verwendet wird.
[ x ! ]
Berechnet die Fakultät einer spezifischen positiven ganzen
Zahl n, wobei n
≦
69.
[ RND ] Erzeugt eine willkürliche Zahl zwischen 0.000 und 0.999
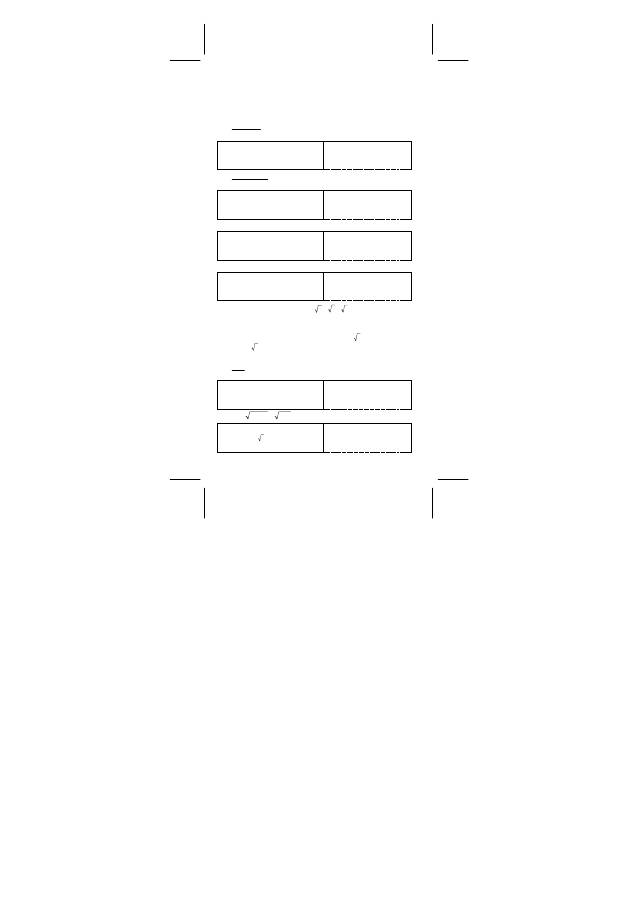
¾
840
!
]
)
4
7
(
[
!
7
=
−
DEG
7 P 4 =
7 [ 2nd ] [ nPr ] 4 [ = ]
8 4 0
.
¾
5
3
!
]
)
4
7
(
[
!
4
!
7
=
−
DEG
7 C 4 =
7 [ 2nd ] [ nCr ] 4 [ = ]
3 5
.
¾
5 ! = 120
DEG
5 ! =
5 [ 2nd ] [ x ! ] [ = ]
1 2 0
.
¾
Erzeugt eine willkürliche Zahl zwischen 0.000 ~ 0.999
DEG
R n d
[ 2nd ] [ RND ]
0
.
4 4 9
Andere Funktionen ( 1/x, ,
3
,
X
, x
2
, x
3
, x
y
, INT,
FRAC )
Der Rechner verfügt über Funktionen für Kehrwert ( [ 2nd ] [ 1/x ] ),
Quadratwurzel ( [
√
] ), Kubikwurzel ( [ 2nd ] [
3
] ), Universalwurzel
( [ 2nd ] [
X
] ), Quadrat ( [ x
2
] ), Kubik ( [ 2nd ] [ x
3
] ) und
Potenzierung ( [ x
y
] ).
¾
8
.
0
.25
1
1
=
DEG
1
.
2 5
–1
=
1.25 [ 2nd ] [ 1 / x ] [ = ]
0
.
8
¾
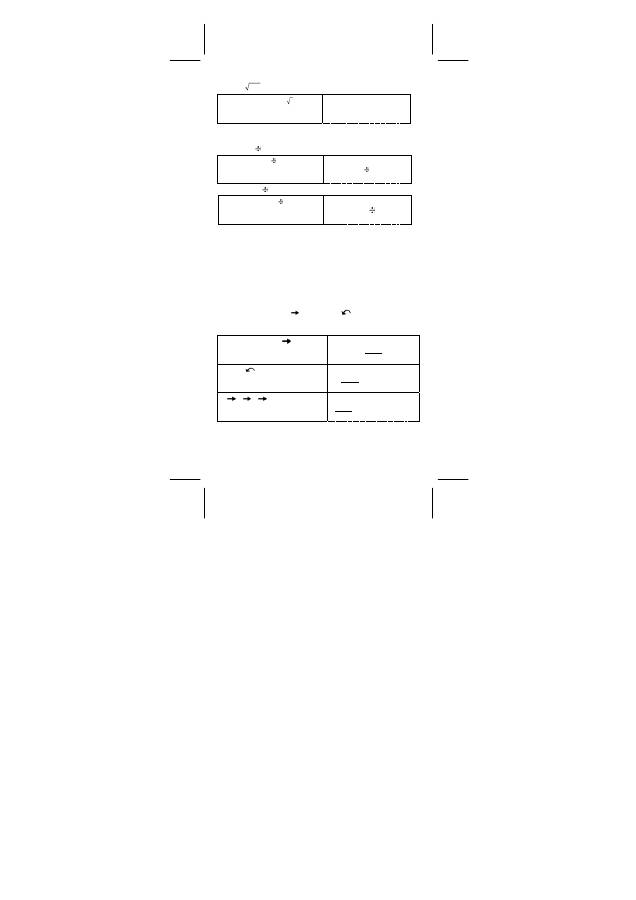
139
=
5
+
125
+
21
+
4
+
2
3
3
2
DEG
2
2
+
√
( 4 + 2 1 ) +
2 [ x
2
] [ + ] [
√
] [ ( ] 4 [ + ] 21 [ ) ]
[ + ] [ 2nd ] [
3
] 125 [ + ] 5 [ 2nd ]
[ x
3
] [ = ]
1 3
9
.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G18-
¾
16812
=
625
+
7
4
5
DEG
7 x
y
5 + 4
X
√
6 2 5 =
7 [ x
y
] 5 [ + ] 4 [ 2nd ] [
X
] 625 [ = ]
1 6 8 1
2
.
INT
Zeigt den Integerteil einer gegebenen Zahl an
FRAC
Zeigt den gebrochenen Teil einer gegebenen Zahl an
¾
INT ( 10 8 ) = INT ( 1.25 ) = 1
DEG
I N T ( 1 0
8 =
[ 2nd ] [ INT ] 10 [ ] 8 [ = ]
1
.
¾
FRAC ( 10 8 ) = FRAC ( 1.25 ) = 0.25
DEG
F R A C ( 1 0
8 =
[ 2nd ] [ FRAC ] 10 [ ] 8 [ = ]
0
.
2 5
Einheitenkonvertierung
Der Rechner arbeitet mit einer integrierten Funktion zur
Einheitenkonvertierung, die Zahlen in andere Einheiten konvertiert.
1. Geben Sie die zu konvertierende Zahl ein.
2. Dr
ü
cken Sie [ CONV ], um ein Menü anzuzeigen. Es gibt 7 Menüs,
Entfernung, Zone, Temperatur, Kapazität, Gewicht, Energie und
Druck.
3. Scrollen Sie mit Hilfe von [ CONV ] durch die Liste der Einheiten
und drücken Sie [ = ], wenn das gewünschte Einheitenmenü
erscheint.
4. Durch Drücken von [
] oder [ 2nd ] [
] wird die Zahl in eine
andere Einheit konvertiert.
¾
1 y d
2
= 9 f t
2
= 0.00000083612 km
2
DEG
f t
2
y d
2
m
2
1 [ CONV ] [ CONV ] [
] [ = ]
1
.
DEG
f t
2
y d
2
m
2
[ 2nd ] [
]
9
.
DEG
k m
2
h e c t a r e s
[
] [
] [
]
0
.
0 0 0 0 0 0 8 3 6 1 2
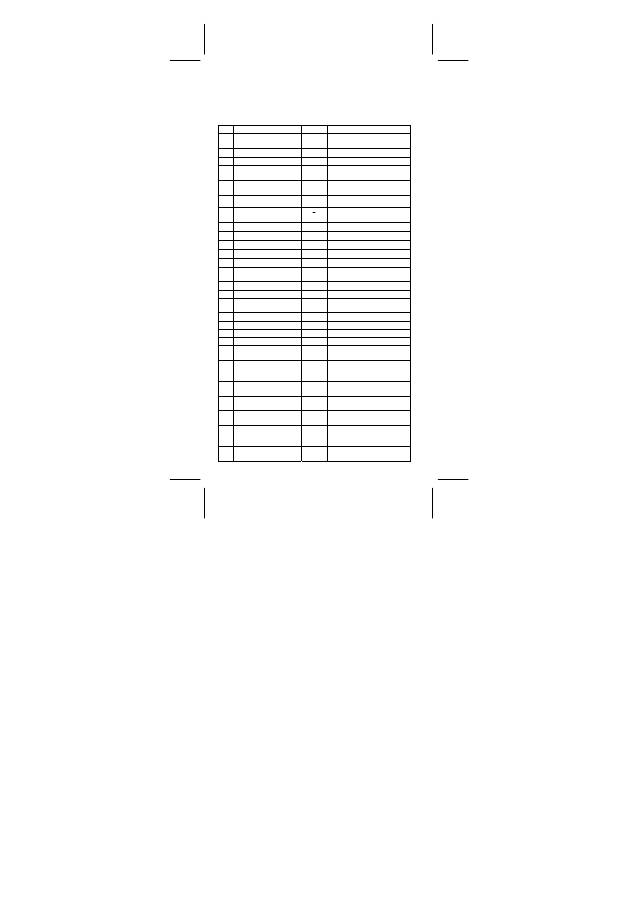
Physikkonstanten
Sie können folgende 136 Physikkonstanten in Ihren Berechnungen
verwenden:
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G19-
Die Daten wurden unter Rückgriff auf Peter J.Mohr und Barry N.Taylor,
CODATA Recommended Values of the Fundamental Physical
Constants:1998, Journal of Physical and Chemical Reference
Data,Vol.28, No.6,1999 und Reviews of Modern Physics,Vol.72, No.2,
2000 erstellt.
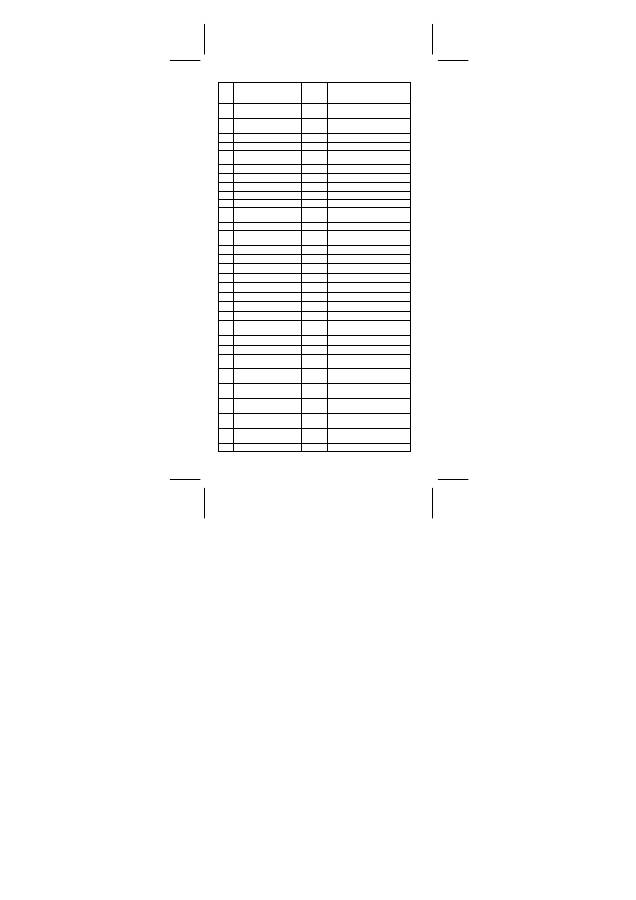
Nr. Bezeichnung Symbol
Wert,
Einheit
1.
Vakuumlichtgeschwindig-
keit
c
299792458 m s
–1
2. Magnetfeldkonstante
μ
0
1.2566370614 x10
–6
N A
–2
3. Elektrische
Konstante
ε
0
8.854187817 x 10
–12
F m
–1
4.
Wellenwiderstand des
Vakuums
Z
0
376.730313461
Ω
5. Gravitationskonstante
G
6.67310 x10
–11
m
3
kg
–
1
s
–
2
6. Planck-Konstante
h
6.6260687652 x10
–34
J s
7.
Planck-Konstante über 2
Pi
h
1.05457159682 x10
–34
J s
8. Avogadro-Konstante
N
A
6.0221419947 x10
23
mol
–1
9. Planck-Elementarlänge
lp
1.616012 x10
–35
m
10. Planck-Elementarzeit
tp
5.390640 x10
–44
s
11. Planck-Masse
mp
2.176716 x10
–8
kg
12. Atomare
Masseneinheit
m
μ
1.6605387313 x10
–27
kg
13.
Atomare Masseneinheit
Energieäquivalent
m
μ
c
2
1.4924177812 x10
–10
J
14. Faraday-Konstante
IF
96485.341539 C mol
–1
15. Elementarladung
e
1.60217646263
x10
–19
C
16.
Elektron Volt–Joule
Verhältnis
eV 1.60217646263
x10
–19
J
17. Elementarladung pro h
e/h
2.41798949195 x10
14
AJ
–1
18. Molare Gaskonstante
R
8.31447215 J mol
–1
K
–1
19. Boltzmann-Konstante
k
1.380650324
x10
–23
J K
–1
20. Molar
Planck-Konstante
N
A
h 3.99031268930x10
–10
Js mol
–1
21.
Sackur–Tetrode-
Konstante
S
0
/R
–
1.164867844
22.
Wien-
Verschiebungsgesetz-
Konstante
b 2.897768651
x10
–3
m K
23.
Gitterparameter in
Silizium
a 543.10208816
x10
–12
m
24.
Stefan–Boltzmann-
Konstante
σ
5.67040040 x10
–8
W m
–2
K
–4
25.
Standardbeschleunigung
der Schwerkraft
g
9.80665 m s
–2
26.
Verhältnis Atomare
Masseneinheit–
Kilogramm
μ
1.6605387313 x10
–27
kg
27.
Erste
Strahlungskonstante
c
1
3.7417710729 x10
–16
Wm
2
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G20-
28.
Erste
Strahlungskonstante für
spektrale Strahlung
c
1
L
1.19104272293x10
–16
Wm
2
sr
–1
29.
Zweite
Strahlungskonstante
c
2
1.438775225 x10
–2
m K
30.
Molares Normvolumen,
ideales Gas
Vm
22.41399639 x10
–3
m
3
mol
–1
31. Rydberg-Konstante
R
∞
10973731.5685 m
–1
32. Rydberg-Konstante in Hz
R
∞
c
3.28984196037 x10
15
Hz
33.
Rydberg-Konstante in
Joules
R
∞
hc
2.1798719017 x10
–18
J
34. Hartree
Energie
E
h
4.3597438134 x10
–18
J
35. Drehimpulsquantum
h/me
7.27389503253 x10
–4
m
2
s
–1
36. Feinstruktur-Konstante
α
7.29735253327 x10
–3
37. Loschmidt-Konstante
n
0
2.686777547
x10
25
m
–3
38. Bohr
Radius
a
0
0.52917720832
x10
–10
m
39.
Magnetisches
Flussquantum
Φ
0
2.06783363681 x10
–15
Wb
40. Quanten-Hall-Leitfähigkeit
G
0
7.74809169628
x10
–5
S
41.
Inverses der Quanten-
Hall-Leitfähigkeit
G
0
–1
12906.4037865
Ω
42. Josephson-Konstante
KJ
483597.89819 x10
9
Hz V
–1
43. Von
Klitzing-Konstante
RK
25812.8075730
Ω
44. Bohr
Magneton
μ
B
927.40089937 x10
–26
J T
–1
45. Bohr Magneton in Hz/T
μ
B/h
13.9962462456 x10
9
Hz T
–1
46. Bohr Magneton in K/T
μ
B/k
0.671713112 K T
–1
47. Kernmagneton
μ
N
5.0507831720 x10
–27
J T
–1
48.
Kernmagneton in MHz/T
μ
N/h
7.6225939631 MHz T
–1
49. Kernmagneton
in
K/T
μ
N/k
3.658263864 x10
–4
K T
–1
50.
Klassischer
Elektronenradius
re
2.81794028531 x10
–15
m
51. Elektronenmasse
me
9.1093818872 x10
–31
kg
52. Energieäquivalent
mec
2
8.1871041464 x10
–14
J
53.
Elektron–Myon-
Massenverhältnis
me/m
μ
4.8363321015 x10
–3
54.
Elektron–Tau-
Massenverhältnis
me/m
τ
2.8755547 x10
–4
55.
Elektron–Proton-
Massenverhältnis
me/mp
5.44617023212 x10
–4
56.
Elektron–Neutron-
Massenverhältnis
me/mn
5.43867346212 x10
–4
57.
Elektron–Deuteron-
Massenverhältnis
me/md
2.72443711706x10
–4
58.
Spezifische Ladung des
Elektrons
–
e/me
–
1.75882017471 x10
11
Ckg
–1
59. Compton
Wellenlänge
λ
c
2.42631021518 x10
–12
m
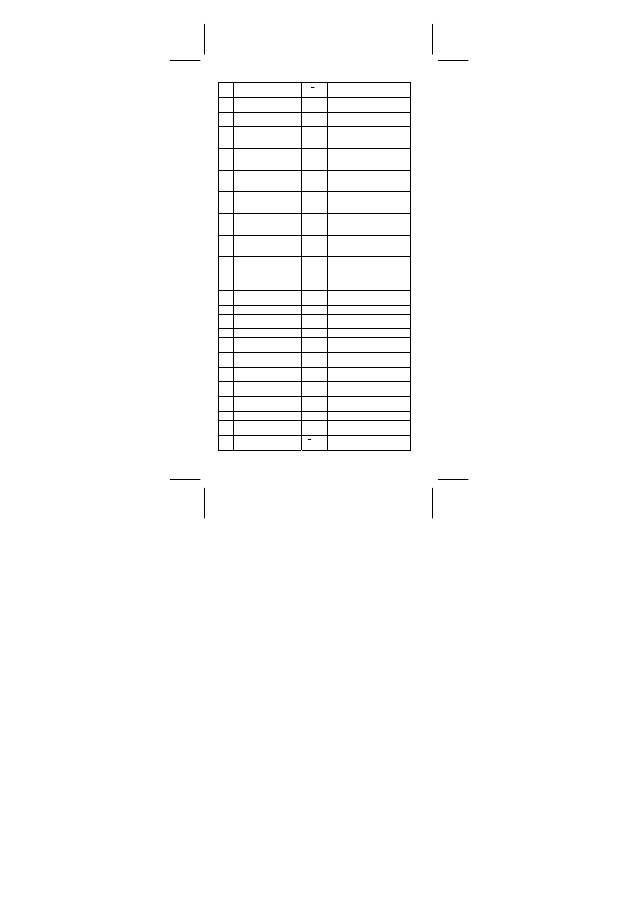
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G21-
60.
Compton Wellenlänge
über 2 Pi
λ
c
386.159264228 x10
–15
m
61.
Thomson-
Wirkungsquerschnitt
σ
e
0.66524585415 x10
–28
m
2
62.
Magnetisches Moment
des Elektrons
μ
e
–
928.47636237x10
–26
J T
–1
63.
Magnetisches Moment
des Elektrons in Bohr
Magnetonen
μ
e/
μ
B
–
1.00115965219
64.
Magnetisches Moment
des Elektrons in Kern
Magnetonen
μ
e/
μ
N
–
1838.28196604
65.
Verhältnis der
Magnetischen Momente:
Elektron–Myon
μ
e/
μ
μ
206.766972063
66.
Verhältnis der
Magnetischen Momente:
Elektron–Proton
μ
e/
μ
p
–
658.210687566
67.
Verhältnis der
Magnetischen Momente:
Elektron–Neutron
μ
e/
μ
n
960.9205023
68.
Verhältnis der
Magnetischen Momente:
Elektron–Deuteron
μ
e/
μ
d
–
2143.92349823
69.
Verhältnis der
Magnetischen Momente:
Elektron
zu
Abschirmmoment des
Helions
μ
e/
μ
'h
864.05825510
70.
Magnetisches Moment
des Elektrons Anomalie
a e
1.15965218694 x10
–3
71. Elektron g–Faktor
g e
–
2.00231930437
72.
Gyromagnetisches
Verhältnis des Elektrons
γ
e
1.76085979471 x10
11
s
–1
T
–1
73. Myonmasse
m
μ
1.8835310916 x10
–28
kg
74.
Myonmasse Energie
Äquivalent
m
μ
c
2
1.6928333214 x10
–11
J
75.
Myon–Tau-
Massenverhältnis
m
μ
/m
τ
5.9457297 x10
–2
76.
Myon–Proton-
Massenverhältnis
m
μ
/mp
0.11260951733
77.
Myon–Neutron
Massenverhältnis
m
μ
/mn
0.11245450793
78.
Myon Magnetisches
Moment Anomalie
a
μ
1.1659160264 x10
–3
79. Myon g–Faktor
g
μ
–
2.00233183201
80.
Compton-Wellenlänge
des Myons
λ
c,
μ
11.7344419735 x10
–15
m
81.
Compton-Wellenlänge
des Myons über 2 Pi
λ
c,
μ
1.86759444455 x10
–15
m
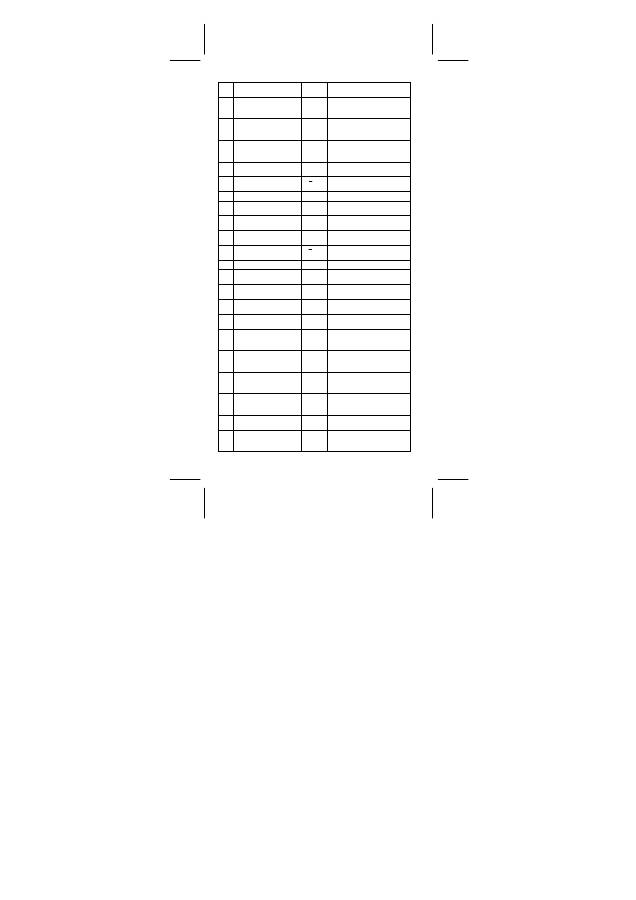
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G22-
82.
Magnetisches Moment
des Myons
μ
μ
–
4.4904481322x10
–26
J T
–1
83.
Magnetisches Moment
des Myons in Bohr
Magnetonen
μ
μ
/
μ
B
–
4.8419708515 x10
–3
84.
Magnetisches Moment
des Myons in Kern
Magnetonen
μ
μ
/
μ
N
–
8.8905977027
85.
Verhältnis der
Magnetischen Momente
Myon–Proton
μ
μ
/
μ
p
–
3.1833453910
86.
Compton-Wellenlänge
des Tauons
λ
c,
τ
0.6977011 x10
–15
m
87.
Compton-Wellenlänge
des Tauons über 2 Pi
λ
c,
τ
0.11104218 x10
–15
m
88. Tau-Masse
m
τ
3.1678852 x10
–27
kg
89.
Tau-Masse
Energieäquivalent
m
τ
c
2
2.8471546 x10
–10
J
90.
Tau–Proton-
Massenverhältnis
m
τ
/mp
1.8939631
91.
Compton-Wellenlänge
des Protons
λ
c,p
1.32140984710 x10
–15
m
92.
Compton-Wellenlänge
des Protons über 2 pi
λ
c,p
0.21030890892 x10
–15
m
93. Proton-Masse
mp
1.6726215813 x10
–27
kg
94.
Proton-Masse
Energieäquivalent
mpc
2
1.5032773112 x10
–10
J
95.
Proton–Neutron-
Massenverhältnis
mp/mn
0.99862347856
96.
Spezifische Ladung des
Protons
e/mp
9.5788340838 x10
7
C kg
–1
97.
Magnetisches Moment
des Protons
μ
p
1.41060663358 x10
–26
J T
–1
98.
Abgeschirmtes
Magnetisches Moment
des Protons
μ
p
1.41057039959 x10
–26
J T
–1
99.
Magnetisches Moment
des Protons in Kern
Magnetonen
μ
p/
μ
N
2.79284733729
100.
Verhältnis der
Magnetischen Momente:
Proton–Neutron
μ
p/
μ
n
–
1.4598980534
101.
Abschirmmoment des
Protons in Bohr
Magnetonen
μ
'p/
μ
B
1.52099313216 x10
–3
102.
Gyromagnetisches
Verhältnis des Protons
γ
p
2.6752221211 x10
8
s
–1
T
–1
103.
Abgeschirmtes
Gyromagnetisches
Verhältnis des Protons
γ
'p
2.6751534111 x10
8
s
–1
T
–1
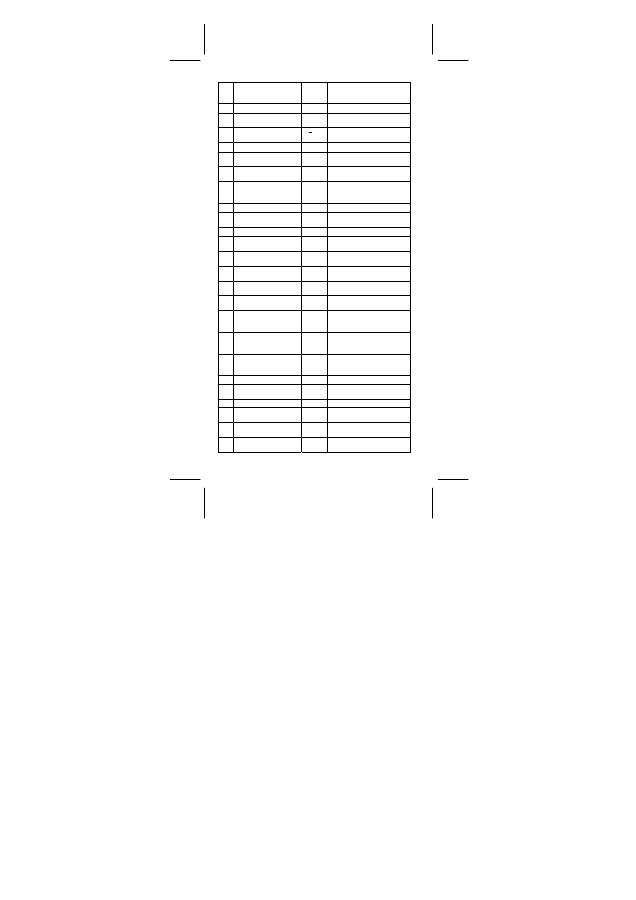
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G23-
104.
Diamagnetische
Abschirmkorrektur für
Protonen
σ
'p
25.68715 x10
–6
105. Proton g–Faktor
g p
5.58569467557
106.
Compton Wellenlänge
des Neutrons
λ
c,n
1.31959089810 x10
–15
m
107.
Compton Wellenlänge
des Neutrons über 2 Pi
λ
c,n
0.21001941422 x10
–15
m
108. Neutronenmasse
mn
1.6749271613 x10
–27
kg
109.
Neutronenmasse
Energieäquivalent
mnc
2
1.5053494612 x10
–10
J
110.
Magnetisches Moment
des Neutrons
μ
n
–
0.9662364023x10
–26
J T
–1
111.
Magnetisches Moment
des Neutrons im Bohr
Magnetonen
μ
n/
μ
B
–1.0418756325 x10
–3
112. Neutron g–Faktor
gn
–
3.8260854590
113.
Gyromagnetisches
Verhältnis des Neutrons
γ
n
1.8324718844 x10
8
s
–1
T
–1
114. Deuteronenmasse
md
3.3435830926 x10
–27
kg
115.
Deuteronenmasse-
Energie Äquivalent
mdc
2
3.0050626224 x10
–10
J
116.
Molare Masse des
Deuterons
M(d) 2.01355321271x10
–3
kg
mol
–1
117.
Deuteron–Elektron
Massenverhältnis
md/me
3670.48295508
118.
Deuteron–Proton
Massenverhältnis
md/mp
1.99900750083
119.
Magnetisches Moment
des Deuterons
μ
d
0.43307345718 x10
–26
J T
–1
120.
Magnetisches Moment
des Deuterons in Bohr
Magnetonen
μ
d/
μ
B
0.46697545565 x10
–3
121.
Magnetisches Moment
des Deuterons in Bohr
Magnetonen
μ
d/
μ
N
0.85743822849
122.
Verhältnis der
Magnetischen Momente
Deuteron–Proton
μ
d/
μ
p
0.30701220835
123. Helion-Masse
mh
5.0064117439 x10
–27
kg
124.
Helion-Masse
Energieäquivalent
mhc
2
4.4995384835 x10
–10
J
125. Helion-Molarmasse
M(h)
3.01493223470x10
–3
kg mol
–1
126.
Helion–Elektron
Massenverhältnis
mh/me
5495.88523812
127.
Helion–Proton
Massenverhältnis
mh/mp
2.99315265851
128.
Abschirmmoment des
Helion
μ
'h
–
1.07455296745 x10
–26
J T
–1
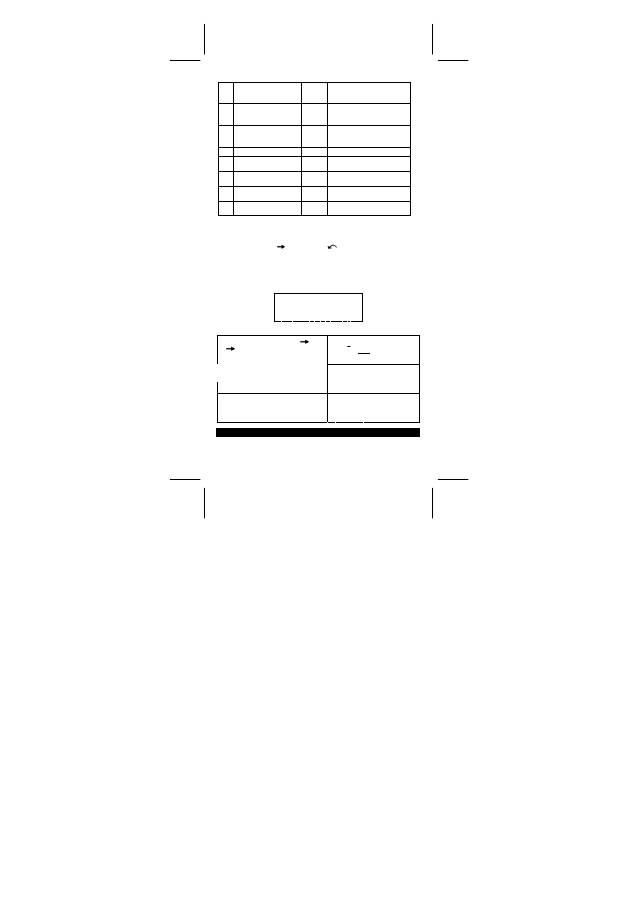
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G24-
129.
Abschirmmoment des
Helion in Bohr
Magnetonen
μ
'h/
μ
B
–
1.15867147414 x10
–3
130.
Abschirmmoment des
Helion in Kern
Magnetonen
μ
'h/
μ
N
–
2.12749771825
131.
Abgeschirmtes
Gyromagnetisches
Verhältnis des Helion
γ
'h
2.03789476485 x10
8
s
–1
T
–1
132. Alpha-Teilchen-Masse
m
α
6.6446559852 x10
–27
kg
133.
Alpha-Teilchen-Masse
Energieäquivalent
m
α
c
2
5.9719189747 x10
–10
J
134.
Molare Masse des Alpha-
Teilchens
M(
α
)
4.00150617471 x10
–3
kg
mol
–1
135.
Alpha-Teilchen-Elektron-
Massenverhältnis
m
α
/me
7294.29950816
136.
Alpha-Teilchen-Proton
Massenverhältnis
m
α
/mp
3.97259968461
Zum Einfügen einer Konstante an der Cursorposition:
1. Dr
ü
cken Sie [ CONST ], um das Menü der Physikkonstanten
anzuzeigen.
2. Dr
ü
cken Sie [
] oder [ 2nd ] [
], bis die gewünschte
Konstante unterstrichen ist.
3. Dr
ü
cken Sie [ = ].
Sie können auch die [ CONST ] Taste zusammen mit einer Zahl von 1
bis 136 nutzen, um die Physikkonstante auszuwählen. Drücken Sie
zum Beispiel 15 [ CONST ].
DEG
e
1
.
6 0 2 1 7 6 4 6 2 6 3
–19
¾
3 x N
A
= 1.80664259841 x 10
24
CONST DEG
h
h
N
A
l p
t p
3 [ x ] [ CONST ] [ CONST ] [
]
[
]
6
.
0 2 2 1 4 1 9 9 4 7
23
CONST DEG
0 0 8
:
m o l
–1
[ = ]
6
.
0 2 2 1 4 1 9 9 4 7
23
CONST DEG
3
¼
N
A
=
[ = ] [ = ]
1
.
8 0 6 6 4 2 5 9 8 4 1
24
Basis–n
Berechnungen
Nutzen Sie für Basis-N Berechnungen MAIN ( [ MODE ] 1 ( MAIN ) )
Modus.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G25-
Der Rechner ist in der Lage Berechnungen mit nicht dezimalen
Zahlenbasen durchzuführen. Binäre, oktale und hexadizimale zahlen
können addiert, subtrahiert, multipliziert und dividiert werden.
Es folgt eine Auflistung der Ziffern, die in jedem Zahlensystem
verwendet werden können.
Binäre Basis ( b ): 0, 1
Oktale Basis ( o ): 0, 1, 2, 3, 4, 5, 6, 7
Dezimale Basis: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hexadezimale Basis ( h ): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
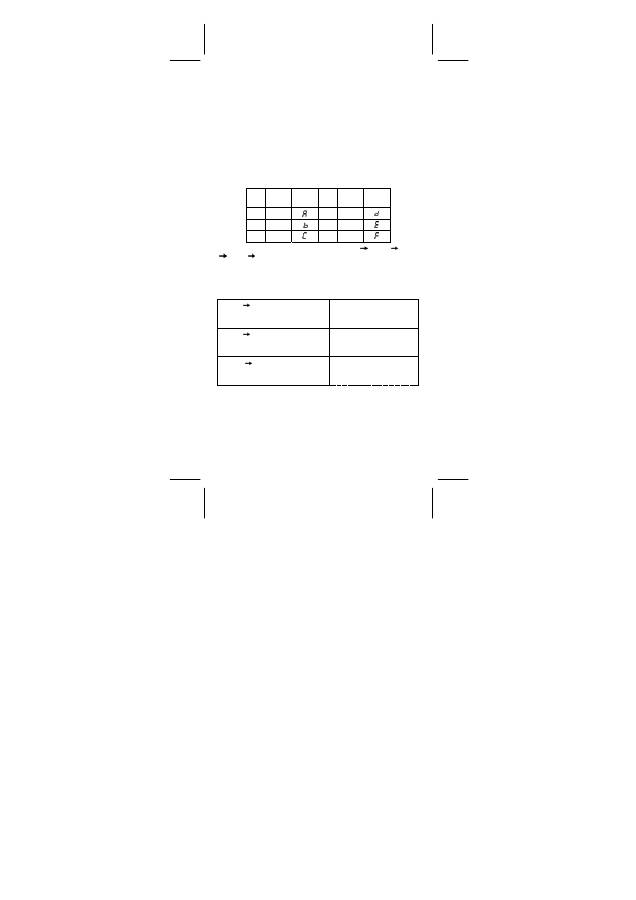
Um A, B, C, D, E und F der hexadezimalen Basis von Standard-
Textzeichen unterscheiden zu können, werden Sie wie folgend
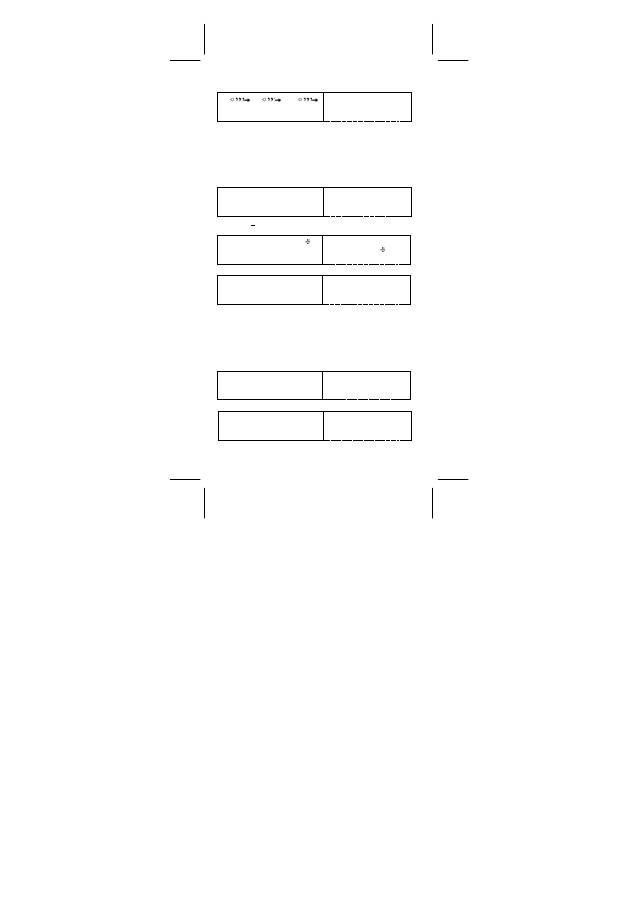
gezeigt dargestellt.
Taste
Anzeige
(Obere)
Anzeige
(Untere)
Taste
Anzeige
(Obere)
Anzeige
(Untere)
A /A
D
ID
B IB
E IE
C
I
C
F IF
Wählen Sie die zu nutzende Zahlenbasis mit [ BIN ], [ OCT ],
[ DEC ], [ HEX ]. Die Indikatoren " BIN ", " b ", " OCT ", " o ", " HEX
", " h " zeigen an, welche Zahlenbasis benutzt wird. Wird keiner der
Indikatoren angezeigt, nutzen Sie eine Dezimalbasis.
Basiskonversionen
¾
37 (Basis 8) = 31 (Basis 10) = 1F (Basis 16)
DEG
OCT
[ 2nd ] [ OCT ] 37
0 0 0 0 0 0 0 0 0 3 7
o
DEG
[ 2nd ] [ DEC ]
3 1
.
DEG
HEX
[ 2nd ] [ HEX ]
0 0 0 0 0 0 1 F
h
Block-Funktion
Ein Ergebnis auf binärer Basis wird unter Verwendung der Block-
Funktion angezeigt. Das Maximum von 32 Ziffern wird in 4 Blöcken à
8 Ziffern angezeigt.
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G26-
1 1 0 1 0 0 1 1
b
DEG BIN
Zeigt die Anzahl der Blöcke: 1 Blöcke
Zeigt an, dass Block 4 zur Zeit angezeigt wird
Zeigt an, dass Block 4 zur Zeit angezeigt wird
Zeigt an, dass Block 4 zur Zeit angezeigt w
Zeigt an, dass Block 4 zur Zeit angezeig
Zeigt die Anzahl der Blöcke: 1 Blöcke
Zeigt die Anzahl der Blöcke: 1 Blöcke
Zeigt die Anzahl der Blöcke: 1 Blöcke
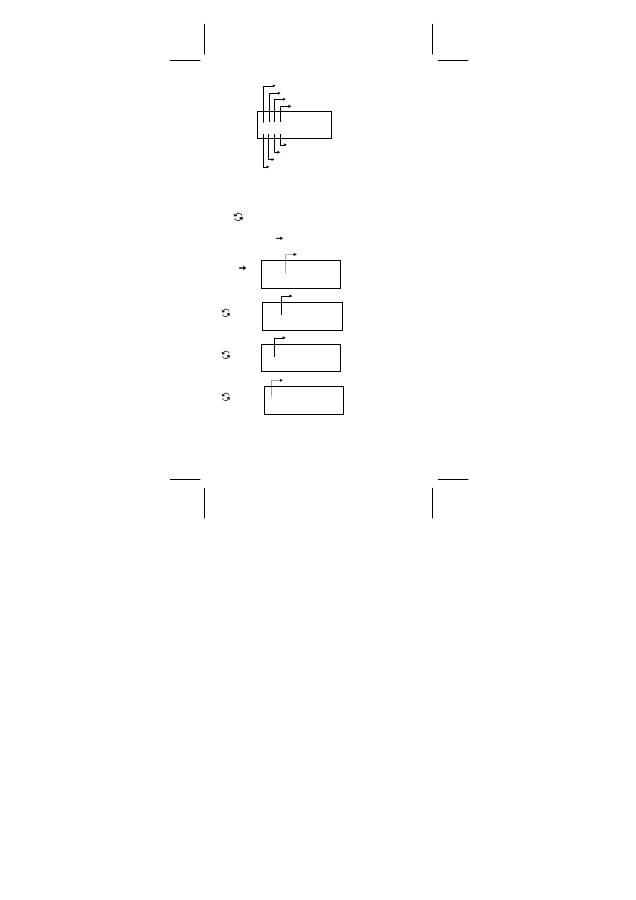
Die Block-Funktion besteht aus oberen und unteren Blockindikatoren.
Der obere Indikator zeigt die aktuelle Blockposition, der untere
Indikator zeigt die gesamten Blöcke für ein Ergebnis.
Bei einer binären Basis wird Block 1 sofort nach der Berechnung
angezeigt. Andere Blöcke ( Block 2 ~ Block 4 ) werden durch Drücken
von [
] angezeigt.
Zum Beispiel, Eingabe 47577557
16
Drücken Sie [ 2nd ] [ HEX ] 47577557
[ 2nd ] [ BIN ]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Zeigt an, dass Block 1 zur Zeit angezeigt wird
[
]
0 1 1 1 0 1 0 1
b
DEG BIN
–
–
Zeigt an, dass Block 2 zur Zeit angezeigt wird
[
]
0 1 0 1 0 1 1 1
b
DEG BIN
– –
Zeigt an, dass Block 3 zur Zeit angezeigt wird
[
]
0 1 0 0 0 1 1 1
b
DEG BIN
– – –
Zeigt an, dass Block 4 zur Zeit angezeigt wird
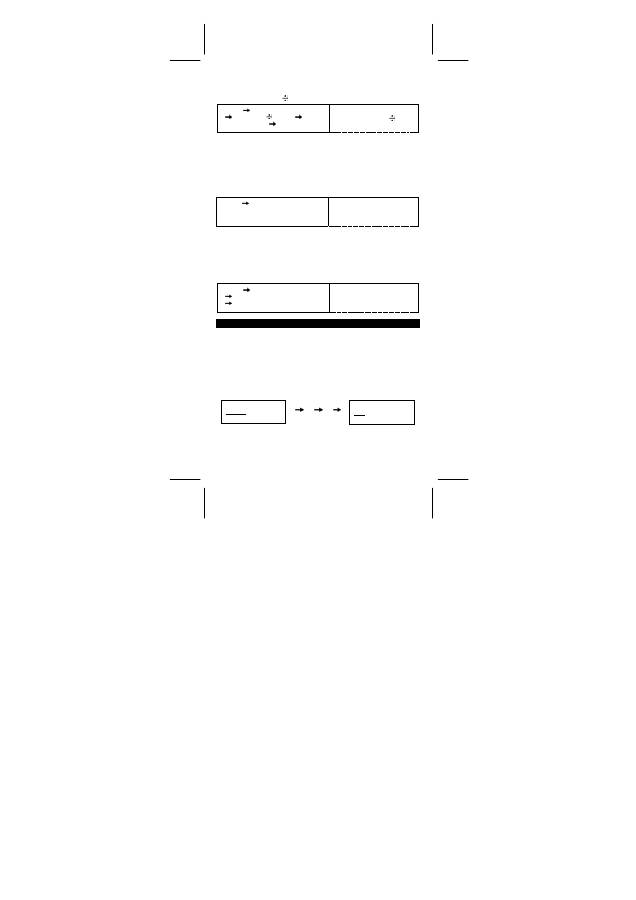
47577557
16
= Block 4 + Block 3 + Block 2 + Block 1
= 01000111010101110111010101010111
2
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G27-
Grundlegende arithmetische Operationen für Basen
¾
1IEIF
16
+ 1234
10
1001
2
= 1170
8
DEG
OCT
h 1 IE IF + 1 2 3 4
b 1
[ 2nd ] [ HEX ] 1E F [ + ] [ 2nd ]
[ DEC ] 1234 [ ] [ 2nd ] [ BIN ]
1001 [ = ] [ 2nd ] [ OCT ]
0 0 0 0 0 0 0 1 1 7 0
o
Negative Werte
Bei binären, oktalen und hexadezimalen Basen, zeigt der Rechner
negative Zahlen mit Hilfe der Komplementdarstellung an. Das
Komplement ist das Ergebnis der Subtraktion dieser Zahl von
100000000000000000000000000000000 in dieser Zahlenbasis durch
drücken der [ NEG ] Taste bei nicht-dezimalen Basen.
¾
3/A
16
= NEG IFIFIFIFIFIFIC6
16
DEG
HEX
N E G
h 3 /A
[ 2nd ] [ HEX ] 3 A [ NEG ]
F F F F F F C 6
h
Logische Operation
Logische Operationen werden mit Hilfe logischer Produkte (AND),
negativer logischer (NAND), logischer Summen (OR), exklusiver
logischer Summen (XOR), Negation (NOT) und Negationen von
exklusivenlogischen Summen (XNOR) durchgeführt.
¾
1010
2
AND ( /A
16
OR 7
16
) = 12
8
DEG
OCT
b 1 0 1 0
A N D
( h
[ 2nd ] [ BIN ] 1010 [ AND ] [ ( ] [ 2nd ]
[ HEX ] A [ OR ] 7 [ ) ] [ = ] [ 2nd ]
[ OCT ]
0 0 0 0 0 0 0 0 0 1 2
o
Statistische
Berechnungen
Wählen Sie den STAT ( [ MODE ] 2 ( STAT ) ) Modus für statistische
Berechnungen.
Dieser Modus dient der Ausführung von einzelvariablen und
paarvariablen statistischen Berechnungen.
Dr
ü
cken Sie [ MODE ] 2 ( STAT ), um den STAT Modus zu wählen.
Sie können eines der sechs im STAT Modus vorhandenen
Untermenüs auswählen,
DEG
1–VAR LIN LOG
STAT
[
] [
] [
]
DEG
EXP PWR D–CL
STAT
Einzelvariable Statistik
1–VAR Einzelvariable
Statistik
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G28-
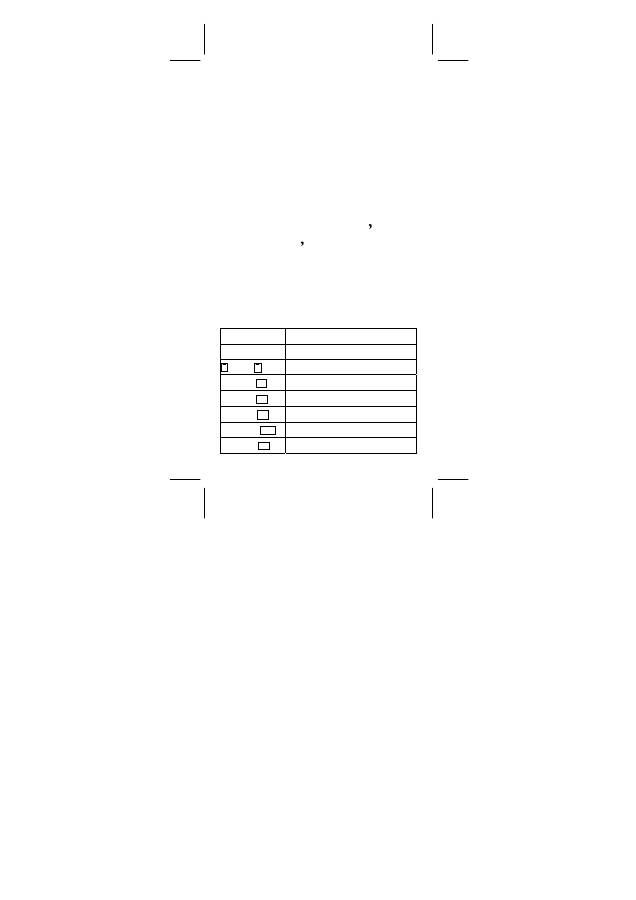
Paarvariable / Regressionsstatistik
LIN
Lineare Regression
y = a + b x
LOG
Logarithmische Regression
y = a + b lnx
EXP
Exponentialregression
y = a • e
bx
POW
Potenzregression
y = a • x
b
D–CL
Alle statistischen Daten löschen
Dateneingabe
Vergessen Sie nicht vor der Ausführung einer statistischen
Berechnung mit D–CL alte Daten zu löschen.
(A) Folgende Syntax dient zur Eingabe einzelvariabler Daten:
# Individuelle Daten: [ DATA ] < x-Daten >
# Multiple Daten des gleichen Werts:
[ DATA ] < x-Daten > [ x ] < Anzahl der Wiederholungen >
(B) Folgende Syntax dient zur Eingabe paarvariabler /
Regressionsdaten:
# Individuelles Datenset: [ DATA ] < x-Daten > [ ] < y-Daten >
# Multiple Daten des gleichen Wertes:
[ DATA ] < x-Daten > [ ] < y-Daten > [ x ] < Anzahl der
Wiederholungen >
(Hinweis): Auch beim Verlassen des STAT Modus bleiben alle Daten
erhaltend, solange sie nicht mit dem D-CL Modus gelöscht
werden.
Ergebnisanzeige
Die Werte der statistischen Variablen hängen von den eingegebenen
Daten ab. Die folgende Tabelle gibt Auskunft über die verwendeten
Tastenkombinationen.
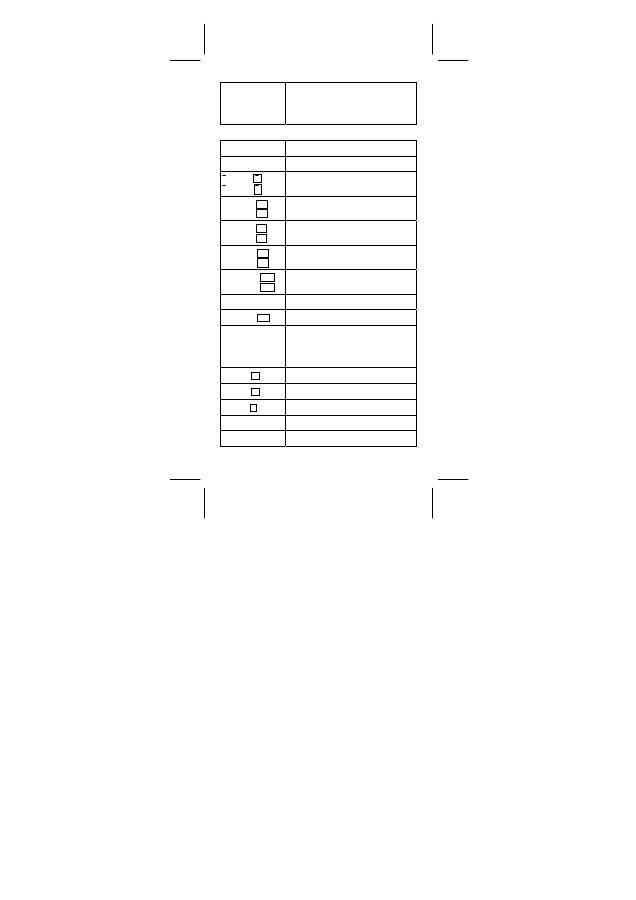
Einzelvariable statistische Berechnungen
Variablen Bedeutung
n ( [ n ] )
Anzahl der eingegebenen x-Daten
x
( [2nd]+[
x
] )
Mittelwert der x-Daten
Sx
( [2nd]+[
Sx
] )
Auswahl-Standardabweichung für x-Daten
σ
x
( [2nd]+[
σ
x
] )
Bevölkerungs-Standardabweichung für x-
Daten
∑
x
( [2nd]+[
∑
x
] )
Summe aller x-Daten
∑
x
2
( [2nd]+[
∑
x
2
]) Summe aller x
2
Daten
CP
( [2nd]+[
CP
] )
Potentielle Präzisionsfähigkeit für x-Daten
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G29-
CPK ( [CPK] )
Minimum (CPU, CPL) für x-Daten, wobei die
CPU die obere und CPL die untere
Bestimmungsgrenze der Präzisionsfähigkeit
ist
CPK = Min ( CPU , CPL ) = CP ( 1 – Ca )
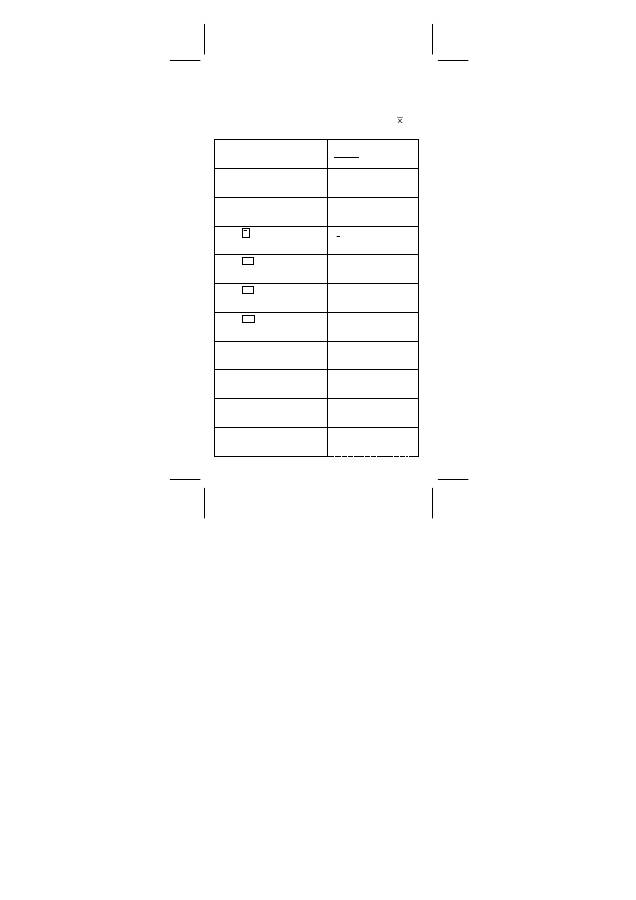
Paarvariable Statistik / Regressionsberechnung
Variablen Bedeutung
n ( [ n ] )
Anzahl der eingegebenen x-y Paare
x
( [2nd]+[
x
] )
y
( [2nd]+[
y
] )
Mittelwert der x-Daten oder y-Daten
Sx
( [2nd]+[ Sx ] )
Sy
( [2nd]+[ Sy ] )
Auswahl-Standardabweichung für x-Daten
und y-Daten
σ
x
( [2nd]+[
σ
x
] )
σ
y
( [2nd]+[
σ
y
] )
Potentielle Präzisionsfähigkeit für x-Daten
oder y-Daten
∑
x
( [2nd]+[
∑
x
] )
∑
y
( [2nd]+[
∑
y
] )
Summe aller x-Daten oder y-Daten
∑
x
2
( [2nd]+[
∑
x
2
])
∑
y
2
( [2nd]+[
∑
y
2
])
Summe aller x
2
Daten oder y
2
Daten
∑
x y
Summe ( x • y ) für alle x-y Paare
CP
( [2nd]+[
CP
] )
Potentielle Präzisionsfähigkeit für x-Daten
CPK ( [ CPK ] )
Minimum (CPU, CPL) für x-Daten, wobei
CPU die obere, CPL die untere
Bestimmungsgrenze der Präzisionsfähigkeit
ist
CPK = Min ( CPU , CPL ) = CP ( 1 – Ca )
a ( [2nd]+[
a ] )
Konstanter Ausdruck a der
Regressionsformel
b ( [2nd]+[
b ] )
Regressionskoeffizient b der
Regressionsformel
r ( [2nd]+[
r ] )
Korrelationskoeffizient r
x
’
([ x
’
] )
Geschätzter Wert von x
y
’
([ y
’
] )
Geschätzter Wert von y
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G30-
Neue Daten können jederzeit hinzugefügt werden. Der Rechner
berechnet automatisch den Wert neu, wenn [ DATA ] gedrückt wird
und ein neuer Wert eingegeben wird.
¾
Geben Sie ein: USL
= 95, LSL = 70, DATA 1 = 75, DATA 2 = 85,
DATA 3 = 90, DATA 4 = 82, DATA 5 = 77, dies ergibt n = 5, =
81.8, Sx = 6.05805249234,
σ
x = 5.41848687366, CP =
0.76897236513, und CPK = 0.72590991268
DEG
STAT
1–
V A R
L I N
L O G
[ MODE ] 2
DEG
STAT
D A T A
5
[ = ] [ DATA ] 75 [ DATA ] 85 [ DATA ] 90
[ DATA ] 82 [ DATA ] 77
7 7
DEG
STAT
n
[ n ]
5
.
DEG
STAT
x
[ 2nd ] [ x
]
8 1
.
8
DEG
STAT
S x
[ 2nd ] [ Sx ]
6
.
0 5 8 0 5 2 4 9 2 3 4
DEG
STAT
σ
x
[ 2nd ] [
σ
x ]
5
.
4 1 8 4 8 6 8 7 3 6 6
DEG
STAT
U S L =
[ 2nd ] [ CP ] 95
9 5
CP
USL
DEG
STAT
L S L =
[ = ] 70
7 0
CP
LSL
DEG
STAT
C P
[ = ]
0
.
7 6 8 9 7 2 3 6 5 1 3
DEG
STAT
U S L =
[ CPK ]
9 5
.
CPK
USL
DEG
STAT
L S L =
[ = ]
7 0
.
CPK
LSL
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G31-
DEG
STAT
C P K
[ = ]
0
.
7 2 5 9 0 9 9 1 2 6 8
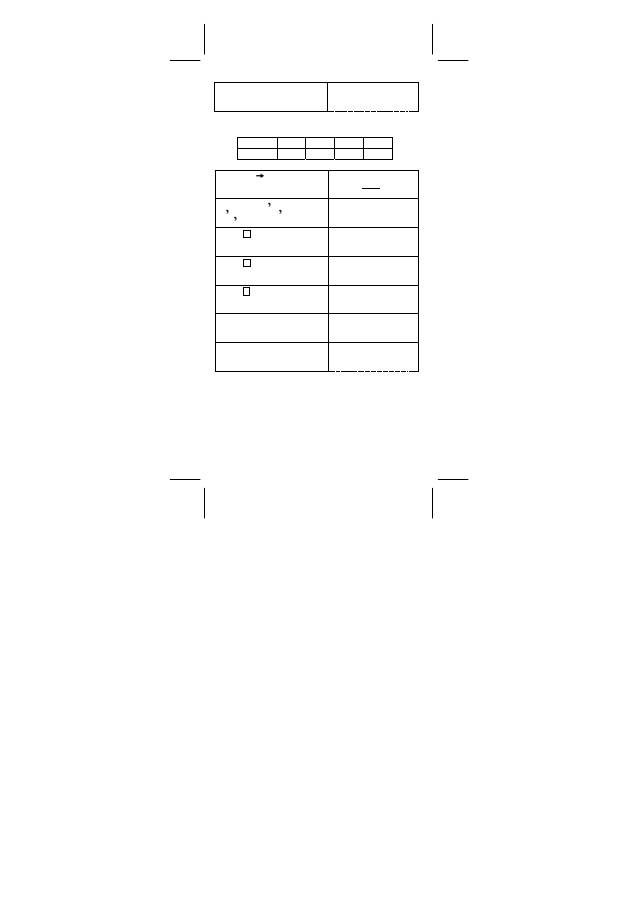
¾
Finden Sie a, b und r für folgende Daten, nutzen Sie lineare
Regression und Schätzwert x = ? für y =573 und y = ? für x = 19.
Datenposten
15 17 21 28
FREQ. 451 475 525 678
DEG
STAT
1–
V A R
L I N
L O G
[ MODE ] 2 [
]
DEG
STAT
D A T A
4 = 2 8
,
[ = ] [ DATA ] 15 [ ] 451 [ DATA ] 17
[ ] 475 [ DATA ] 21 [ ] 525 [ DATA ]
28 [ ] 678
6 7 8
REG
DEG
STAT
a
[ 2nd ] [ a ]
1 7 6
.
1 0 6 3 2 9 1 1 4
REG
DEG
STAT
b
[ 2nd ] [ b ]
1 7
.
5 8 7 3 4 1 7 7 2 2
REG
DEG
STAT
r
[ 2nd ] [ r ]
0
.
9 8 9 8 4 5 1 6 4 1 3
REG
DEG
STAT
x
’
5 7 3
573 [ x
’
]
2 2
.
5 6 7 0 0 7 3 4 1 3
REG
DEG
STAT
y
’
1 9
19 [ y
’
]
5 1 0
.
2 6 5 8 2 2 7 8 5
REG
Daten löschen
Die Löschmethode richtet sich danach, ob die Daten bereits durch
Drücken der [ DATA ] Taste gespeichert wurde, oder nicht.
Um Daten zu löschen, die gerade eingegeben, aber noch nicht durch
Drücken der [ DATA ] Taste gespeichert wurden, dr
ü
cken Sie einfach
[ CE ].
DATA ] Taste gespeichert wurde, oder nicht.
Um Daten zu löschen, die schon durch Drücken der [ DATA ] Taste
gespeichert wurden,
(A) Einzelvariable Daten werden mit folgender Syntax gelöscht:

SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G32-
# < x Wert > [ 2nd ] [ DEL ]
# < x Wert > [ x ] < Anzahl der Wiederholungen > [ 2nd ] [ DEL ]
(B) Paarvariable / Regressionsdaten werden mit folgender Syntax
gelöscht:
# Individuelles Datenset: < x Wert > [ ] < y Wert > [ 2nd ] [ DEL ]
# Multiples Datenset mit gleichem Wert:
< x Wert > [ ] < y Wert > [ x ] < Anzahl der Wiederholungen >
[ 2nd ] [ DEL ]
Wird ein Wert eingegeben und gelöscht, der durch einen Fehler nicht
Teil der gespeicherten Daten ist, erscheint die Fehlermeldung " dEL
Error ", die vorherigen Daten bleiben dabei gespeichert.
Daten bearbeiten
Dr
ü
cken Sie [ 2nd ] [ EDIT ] um den EDIT Modus zu aktivieren. Dieser
Modus ermöglicht einfaches und bequemes Betrachten, Korrigieren
und Löschen von Daten.
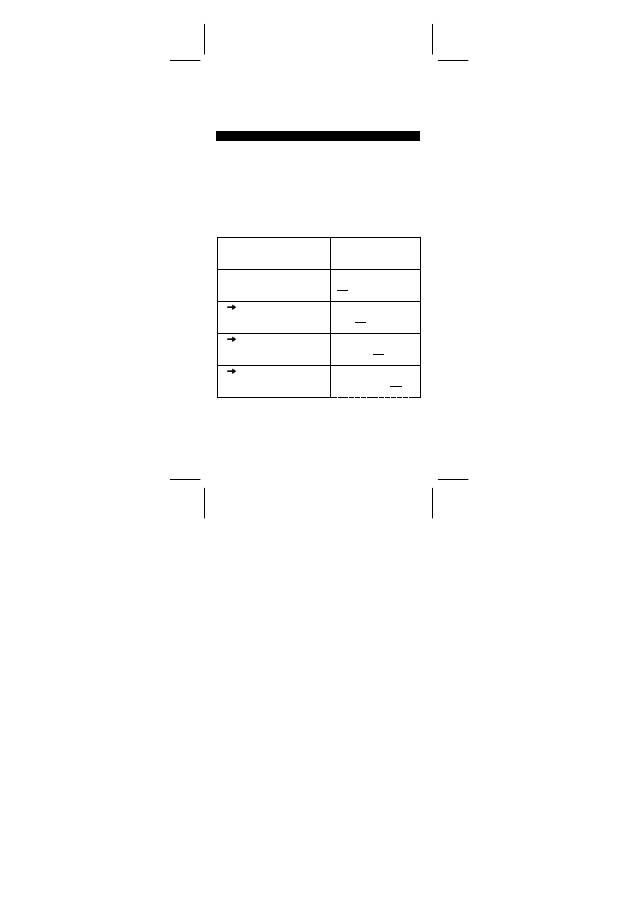
(A) Im 1–VAR Modus hängt die Methode der Datenbetrachtung davon
ab, ob Sie den Datenposten betrachten wollen, oder nicht.
# Bei jedem Drücken von [ DATA ] erscheint erst der Datenposten
1 Sekunde lang und anschließend der entsprechende Wert.
[ DATA ]
DEG
dAtA 1
STAT
EDIT
1 Sekunde
DEG
15.
STAT
EDIT
# Wird [ = ] gedrückt, erscheint der Wert direkt auf dem Bildschirm,
ohne Datenposten.
[ = ]
DEG
15.
STAT
EDIT
(B) Im
REG Modus erscheint immer wenn Sie [ DATA ] drücken der
Datenposten und x Wert gleichzeitig auf dem Bildschirm. Drücken
Sie [ ], um zwischen x und y Wert zu wechseln.
[ DATA ]
DEG
DATA 1 = 15 , 45
STAT
15
EDIT
[ ]
DEG
DATA 1 = 15 , 45
STAT
451
EDIT
Um Daten zu korrigieren, suchen Sie einen neuen Eintrag, um den
alten zu ersetzen.
Der Hinweis FULL
Der Hinweis “FULL” wird angezeigt, wenn einer der folgenden
Bedingungen auftritt; weitere Dateneingabe ist unmöglich. Durch
Drücken einer beliebigen Taste kann der Hinweis gelöscht werden.
Vorherige Dateneinträge bleiben erhalten, solange der STAT Modus
nicht verlassen wird.
1) Falls die Anzahl der Dateneingaben durch [ DATA ] 50 übersteigt
SR260B_SR-281N_German_v090330.doc SIZE:140x75mm SCALE 1:1
2009/3/30
-G33-
2) Falls die Anzahl der Wiederholungen 255 übersteigt
3) n
>
12750 (n = 12750 erscheint, wenn die Anzahl der
Dateneingaben durch [ DATA ] bis zu 50 und die Anzahl der
Wiederholungen eines Wertes 255 beträgt, d.h. 12750 = 50 x
255 )
Komplexe
Berechnungen
Nutzen Sie den CPLX ( [ MODE ] 3 ( CPLX ) ) Modus für komplexe
Berechnungen.
Dieser Modus ermöglicht das Addieren, Substrahieren, Multiplizieren
und Dividieren komplexer Zahlen.
Ergebnisse einer komplexen Operation werden auf folgende Weise
dargestellt:
Re
Realer Wert
Im
Fiktiver Wert
ab Absoluter
Wert ar Beweiswert
¾
( 7 – 9 i ) + ( 15 + 12 i ) = 22 + 3 i , ab = 22.2036033112, ar =
7.76516601843
CPLX
DEG
[ MODE ] 3
0
.
CPLX
DEG
R e
I m
a b
a r
7 [ – ] 9 [ i ] [ + ] 15 [ + ] 12 [ i ] [ = ]
2 2
.
CPLX
DEG
R e
I m
a b
a r
[
]
3
.
i
CPLX
DEG
R e
I m
a b
a r
[
]
2 2
.
2 0 3 6 0 3 3 1 1 2
CPLX
DEG
R e
I m
a b
a r
[
]
7
.
7 6 5 1 6 6 0 1 8 4 3
Оглавление
- Contents
- CONTENIDOS
- Índice
- Inhaltsverzeichnis
- Sommaire
- Indice
- Indhold
- Содержание
- Zawarto ść

